Converted document

FREE BODY DIAGRAMS

Example 1: Equilibrium
Consider the box of weight, W on the ramp:
figure images/equil-ex1.png
Figure 1 Box tethered on a ramp.
The chord is holding the box at the current position of the figure. What is the free body diagram for this equilibrium analysis?
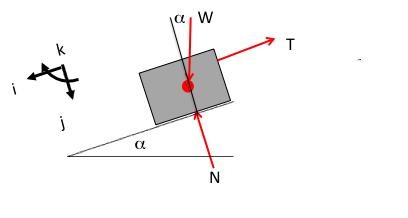
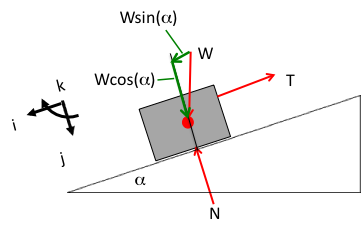
In this example, motion is down the ramp, so the use of a Cartesian frame oriented parallel and normal to the ramp is most appropriate, as shown in Fig. 2↓. The weight is the only force that is not used immediately in the frame of reference. For equilibrium, the tension, T, must balance the component of the box weight that is parallel and down the ramp, as illustrated in Fig. 3↓.
figure images/fbd1-ex1.png
Figure 2 Free body diagram of the body on a ramp.

figure images/fbd2-ex1.png
Figure 3 Free body diagram of the body on a ramp with decomposition of the weight vector.

Here, while the vector arrows are not to scale (and this is not a problem!), the equations of motion in equilibrium are very easy to write when looking at Fig. 3↑:
i: 0  =  Wsin(α) − T       j: 0  =  Wcos(α) − N       k: 0  =  0
or more simply
i: T  =  Wsin(α)       j: N  =  Wcos(α)      
The equation in the k direction is zero since there are no explicit external forces in that direction.
Example 2: Dynamic Motion
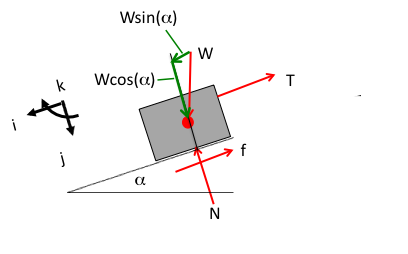
If T < Wsin(α) and the string breaks, then the box will slide down the ramp. The resulting FBD for this motion is different from the FBD for the prior example. Specifically, the FBD should include a new force for the friction, f, as shown in Fig. 4↓.
figure images/fbd1-ex2.png
Figure 4 Free body diagram of the body moving down a ramp.

The equations of motion are now:
i: (W ⁄ g)ẍ  =  Wsin(α) − T − f       j: 0  =  Wcos(α) − N       k: 0  =  0
There is motion down the ramp in the i direction, so there is a nonzero motion (∑F = ma). An additional force for the friction, f is added parallel to the ramp surface. The box does not move through the ramp, so the j remains zero, as does the k motion. The solution of these equations are not as straight forward as that for equilibrium, but the FBD reflects this point.