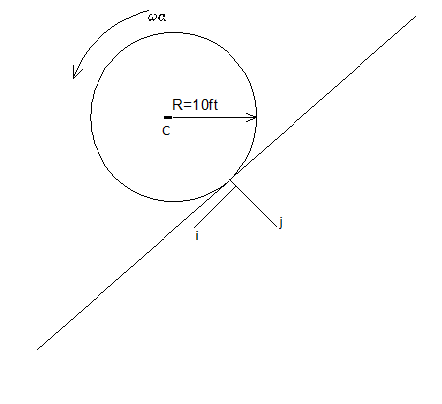
EXAMPLE: ROLLING CYLINDER

Consider the midplane of a homogeneous cylinder rolling down an incline. The radius of the cylinder is 10 feet. It has at the instant of the figure, an angular rotation of ω = 2(r)/(s) and an angular acceleration of α = 3(r)/(s²), both counterclockwise.

a) Find the point in the plane where there is zero acceleration.
b) Using only symbols and integration, compute the moment of inertia about the out of plane axis (z) axis at the point where the cylinder touches the inclined plane, if the density of the cylinder is ρ = ρ₀⎛⎝1 − (r)/(2R)⎞⎠ and the length of the cylinder is T.

figure images/Rolling_cylinder_quiz4_no_origin-1.png

Solution

a) This problem can be solved using the two-dimensional acceleration equation

a_Q = a_P + θ̈k × r_PQ − θ̇² r_PQ

The free body diagram of the figure, along with the coordinate system, is shown in Fig. 2↓.

figure images/Rolling_cylinder_quiz4.png

Figure 2 Free body diagram with coordinate system.

If the origin is set to O and substituting variables yields

a₀ = a_C + α × r_CO − ω² r_CO

a_C = α × r_IC = 3 k × ( − 10 j) = + 30 i

Where C is the center of the cylinder, IC is the instantaneous center and r_CO is the unknown direction vector to location of zero acceleration:

0 = a_O = + 30 i + 3 k × r_CO − 4r_CO = + 30 i + 3xj − 3yi − 4xi − 4yj

This equation can be decomposed into two equations, which can be solved simultaneously:

i: + 30 = 4x + 3y × 4 120 = 16x + 12y 3x − 4y = 0 j: 0 = 3x − 4y × 3 + 0 = 9x − 12y 3⎛⎝(24)/(5)⎞⎠ − 4y = 0 120 = 25x, x = (24)/(5) y = (18)/(5)

Replacing these values into the original position equation, the position vector is

r_CO = (24)/(5) i + (18)/(5) j