POWER FOR AN INSTANTANEOUS CENTER

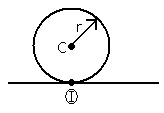
Find the power for a rolling circular body, as seen in Figure 1↓.

Figure 1 Circular body of radius r with coordinate axes originating at center point C and an instantaneous center I.

Figure 1↑ depicts a rolling cylindrical body where the velocity of the center v_C is moving along one axial direction (v_C = v_Ci for example). To derive the kinetic energy for this example, see Kinetic Energy of an Instantaneous Center.

The rate of change of kinetic energy is equivalent to power: P = KĖ; thus power will be:

(dKE)/(dt) = (d)/(dt)⎛⎝(1)/(2)mv_C⋅v_C + (1)/(2)I_c(ωk)⋅(ωk)⎞⎠ = (1)/(2)(mv_C⋅a_C)2 + (1)/(2)I_C(αk⋅ωk)2 = ma_c⋅v_C + I_Cαk⋅(ωk) = ΣF⋅v_C + ΣM_C(ωk) = F₁v₁ + F₂v₂ + ⋯ + (M₁ + M + 2 + ⋯)⋅ωk

Here, I_C is the moment of inertia about point C, m is the mass of the body, and d is the distance from point C to point I. These calculations assume that the body MUST be rigid (the body does not deform or bend).