THE DERIVATIVE

The derivative of a function is a measure of the rate of change of a function’s value as the independent variable (the input) is changed. The simplest case to consider, which helps understand the concept, is the case of a straight line. For a straight line, the slope is a measure of how much the function value changes as the input changes, or

so the derivative of a straight line is equivalent to the slope of the line. In general, however, the derivative of a function is not constant but varies for different values of the input. For example, the derivative may have one value for x = 1 and a different value for x = 2. Nonetheless, the concept of the derivative as the slope is still meaningful if it is understood that for most functions, the slope changes from one point to the next. Consider Fig. 1↓ below, which shows a graph of the function f(x) = sinx + 1:

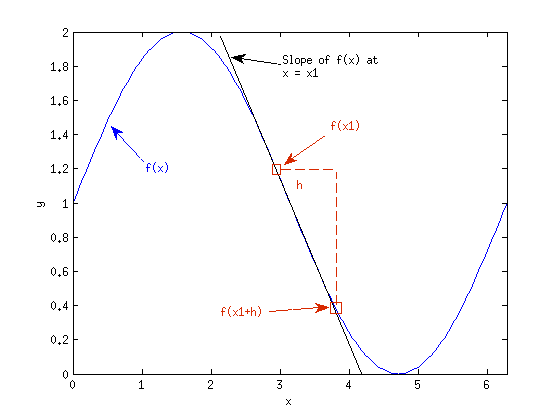
In this figure, the derivative is being sought at x = x1. The local slope of f(x) at this point is drawn; it is a line tangent to the function f(x) at x = x1. It is clear from this figure that the slope (and therefore the derivative) changes as the input x changes. If a tangent line were drawn at x = π ⁄ 2, the line would be horizontal, indicating that the derivative is 0 there. In Fig. 1↑, the derivative is initially large, but it decreases for 0 ≤ x < π. At x = π, the magnitude of the derivative is again relatively large, but it is negative. For π ≤ x < 2π the derivative increases again and at x = 2π it is once again equal to the derivative at x = 0. This cyclical nature of the derivative should not be surprising, considering the function itself is a sinusoidal function. It will be shown how to compute derivatives next.

Mathematically, the concept of the slope is also useful. Consider again the function shown in Fig. 1↑. The slope of the function may be approximated at x1 by fitting a line between f(x1) and f(x1 + h), provided h is not too large. This approximation is valid because the slope of this fitted line is close to the slope of the line tangent to the function f(x) at x = x1. Therefore, we can approximate the derivative at x = x1 as

where f’(x1) is the derivative of f at x1. The reason why this expression is only an approximation of the derivative is because the line between f(x1) and f(x1 + h) is actually a secant line; it is not tangent to the curve at x1. However, the approximation could be improved by decreasing the value of h. If h is very small, then the approximation in Eq. 2↑ is very close to the actual derivative. It follows, then, that if h approaches 0, Eq. 2↑ approaches the derivative of f(x) at x1. Following this logic, the definition of the derivative is

The definition in Eq. 3↑ can be used to compute the derivative of a function at a given point.