DOT PRODUCTS
The dot product is an algebraic operation that multiplies two vectors and returns a scalar. The scalar is obtained by multiplying the magnitudes of each coordinate direction and then summing those products: C = A⋅B. The physical meaning of the dot product can be described as an operation to determine as the magnitude of a vector in the direction of another.
The dot product of two vectors represents an angular relationship between two vectors; that is, the resulting scalar defines the to the cosine of the angle between the vectors times the lengths of each of the vectors. Consider, the two three-dimensional Cartesian vectors A and B :
(1)
A
=
< a1, a2, a3 > = a1 i + a2 j + a3 k
B
=
< b1, b2, b3 > = b1 i + b2 j + b3 k
Each component in the unit directions i, j, k is multiplied with its corresponding component and added:
(2) A⋅B = a1 i⋅b1 i + a2 j⋅b2 j + a3 k⋅b3 k = (a1b1) + (a2b2) + (a3b3)
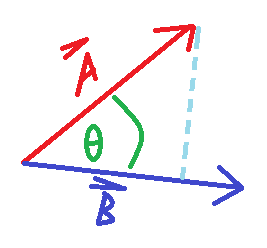
An alternate way of expressing the dot product is via an angular relationship. Consider Fig. 1↑, where θ is defined as the angle between A and B, The dot product can also be expressed as
(3) A⋅B = |A||B|cosθ
where |A| and |B| are the magnitudes of each vector, respectively. From Fig. 1↑, the dot product indicates how closely aligned the vectors are. It is also known as the scalar projection of |A| onto |B|. To illustrate this, consider the dot product of two unit vectors i and i. Since the unit vectors are the same, the angle between them is zero (0), and the dot product becomes
(4) i⋅i = |1||1|cos(0°) = 1
So that the one indicates that the two unit vectors are coincident. Similarly, the dot product of the unit vectors i and j, which are normal or orthogonal to one another, is
(5) i⋅j = |1||1|cos(90°) = 0
where the zero indicates that the two vectors have no directionality in common. A negative value indicates that the two vectors are in opposite directions:
(6) i⋅ − i = |1||1|cos(180°) = − 1
Since the dot product operates on two vectors, but yields a scalar, it is sometimes called a scalar product.
The dot product is not the only multiplicative operation for vectors. The other operation is known as the curl.
Examples of typical dot product problems, as well as applications illustrating the usefulness of the dot product can be found in the remainder of the section.