Converted document

Angular velocity is a vector quantity which is defined for a rigid body or a frame of reference. Let b₁, b₂ and b₃ be three perpendicular unit vectors and form a right-handed frame of reference which is fixed on rigid body B moving in a reference frame A. Angular velocity of the body B is defined as

(1) ω_B ⁄ A = b₁b₂̇⋅b₃ + b₂b₃̇⋅b₁ + b₃b₁̇⋅b₂

Using this definition, if β is a unit vector that is fixed in the rotating frame (or attached to the rigid body) B with respect to A, then the time derivation of β (β̇) is defined as

(2) β̇ = ω_B ⁄ A × β

2D OR PLANAR ANGULAR VELOCITY

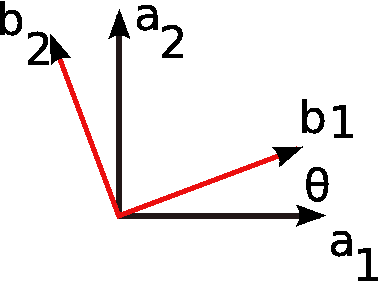
Let frame B (with unit vectors b₁, b₂ and b₃) rotate with respect to frame A (with unit vectors a₁, a₂ and a₃). Figure 1↓ shows a special case when B rotates about b₃, which is also equal to a₃ . (This is a rotation about an the axis normal to the page.) At any point in time, the unit vectors b are oriented at an angle θ with respect to the unit vectors a. The time rate of change of θ is the magnitude of angular velocity. The direction of angular velocity in this case is b₃ = a₃.

Figure 1 Planar angular velocity-- a₁ − a₂ plane

(3) ω_B ⁄ A = θ̇b₃ = θ̇a₃

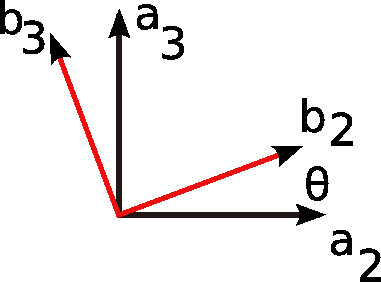
Similarly in the case shown in Fig. 2↓, angular velocity is

(4) ω_B ⁄ A = θ̇b₁ = θ̇a₁

Figure 2 Planar angular velocity-- a₂ − a₃ plane

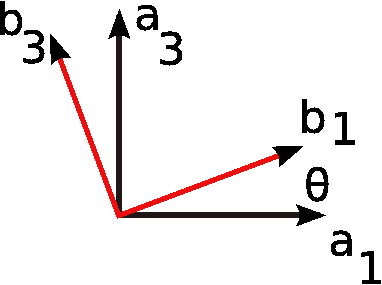
and in the case shown in Fig. 3↓, angular velocity is

(5) ω_B ⁄ A = θ̇b₂ = θ̇a₂

Figure 3 Planar angular velocity-- a₃ − a₁ plane

These cases are called simple rotation.