|
||||||||
 |
 |
 |
 |
|||||
 |
||||||||
 |
||||||||
 |
 |
|||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
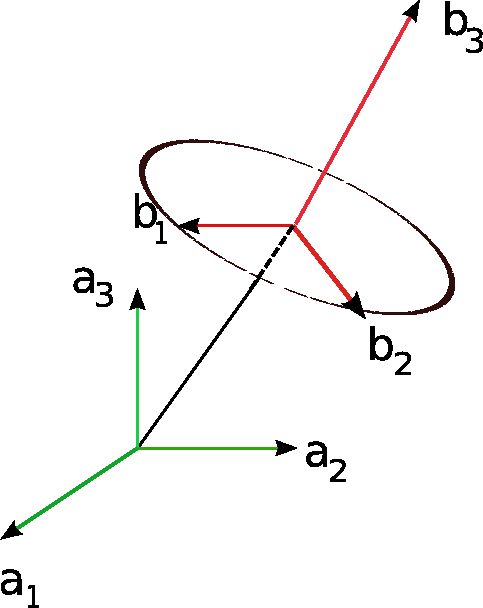
3D ANGULAR VELOCITY
Figure 4↓ shows frame B (the red frame) rotating with respect to frame A (the green frame) about unit vector b2. One can write the angular velocity as
(6)
ωB ⁄ A = θ̇b3
Notice that b3 in this case is not equal to a3. However one can always write b3 in the A frame using the general form b3 = α1 a1 + α2 a2 + α3 a3.
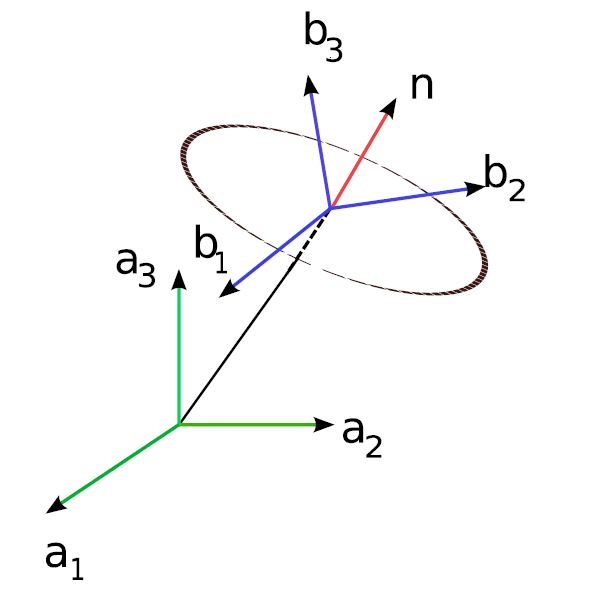
Figure 5↓ shows even a more general case, where the B frame (the blue one) rotates with respect to the A frame about unit vector (n). In this general case there is no such vector as θ, where θ̇ = ωB ⁄ A. However still one can define the angular velocity of frame B with respect to frame A as ωB ⁄ A = θ̇n where n can be decomposed in either frame A or B.
(7)
ωB ⁄ A
= θ̇n
= θ̇(α1 a1 + α2 a2 + α3 a3)
= θ̇(β1 b1 + β2 b2 + β3 b3)
Further explanations are provided on how to apply angular velocity to points on a single body or in different reference frames.
← Previous Page
← Previous Page