TRANSLATIONAL AND ROTATIONAL VELOCITY
These are some basic examples of planar (two-dimensional) bodies in translational and rotation. These provide explanations of the equations discussed in the Theory section.
No examples of translational velocity will be given since when the angular rotation of a body is zero, the velocity of two points on the same body will have the same velocity: VA = VB + ω × rBA = VB + 0.0 × rBA = VB.
Example 1: Body in Rotation
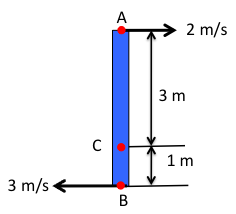
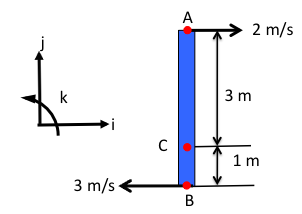
The first step is to identify the the coordinate system. Given the figure, a Cartesian right-handed system will provide simple computations, so that is chosen, and it is illustrated in Fig. 2↓. It is important that the sign convention in the equations follow this system. The k coordinate direction is pointing out of the paper, and there will be rotation in the counterclockwise direction, as noted in the coordinate system figure.
Since the velocities at points A and B on the bar are known, the rotation of the bar can be computed from the equation:
(1) VA = VB + ω × rBA
There are several important items to note about this equation. First, all the terms are in bold, indicating that they are all vectors. Therefore, both the magnitude and direction are important. The rotation of the body will be in the k direction since the body lies in the i and j plane. The vector that indicates the distance from point B to A is denoted as rBA. This is easy to remember since VB is on the right hand side of the equation (starting point) and VA is on the left hand side of the equation (end point).
Substituting in the values from Fig. 1↑, yields
VA
=
VB + ω × rBA
2 m/s i
=
− 3 m/si + ω rad/s k × 4 m j
5 m/s i
=
− 4ω rad/s i
ω
=
− 5 ⁄ 4 rad/s
A good way to check any computation is to include the units, as is illustrated here. The angular velocity is in terms of radians per second. Radians are considered to be “null” units, which is why they disappear when multiplied by the distance unit m. in the second line. Another way to check the computation is to ensure that the unit vectors are the same on both sides of the equation. The cross product results in a negative number (see the cross product section to read how to determine positive and negative values.
The angular velocity applies to the body, so it can be used to compute the velocity at any point on the body. For the instantaneous position of the body in this example (Fig. 2↑), the velocity at point C can be computed using the same relation:
VC
=
VA + ω × rAC
VC m/s i
=
2 m/si + ( − 5 ⁄ 4) rad/s k × − 3 m j
VC m/s i
=
(8 − 15)/(4) m/s i
VC
=
− (7)/(4) m/s
Next Page →
Next Page →