KINETIC ENERGY

Figure 1 Arbitrary body with coordinate axes originating at point C and mass dm for an incremental volume used for integration.

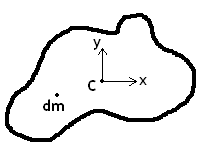
Kinetic energy is associated with the motion of a body or particle and relies on the velocity of the body. The definition of translational kinetic energy (KE) for a three-dimensional body moving in two dimensions (planar motion), as seen in Figure 1↑, is as follows:

(1) KE = (1)/(2)mv² = (1)/(2)⌠⌡( V⋅V)dm

The velocity vector V at an arbitrary point (x,y) is a combination of the velocity at point C and the velocity due to rotation about the z axis on point C. Thus, the velocity is defined as:

(2) V = V_C + ωk × (xi + yj) = V_C + ω( − yi + xj)

where V_C is the velocity vector at point C (the origin of the selected axes) and ωk is the angular velocity with respect to the z axis (i.e. the body is rotating in the x-y plane). The kinetic energy is a positive scalar value (not a vector) that is calculated using the dot product of velocity vectors.

Substituting this dot product into Equation 1↑ results into the following expression:

(3) KE = (1)/(2) V_C⋅V_C⌠⌡dm + (ω²)/(2)⌠⌡(x² + y²)dm − ω(V_C⋅i)⌠⌡ydm + ω(V_C⋅j)⌠⌡xdm

Since the following integrals are zero:

(4) ⌠⌡ydm = ⌠⌡xdm = 0

kinetic energy simplifies to the following equation:

(5) KE = (1)/(2)m(V_C⋅V_C) + (1)/(2)I^C_zzω²

This expression has a component relating to translational motion, (1 ⁄ 2)m(V_C⋅V_C), and another to rotational motion, (1 ⁄ 2)I^C_zzω². Again, note that the kinetic energy is a scalar value, and has the units of a force times a distance, such as ft⋅lb or Joules (N⋅m).