Welcome to AE Resources

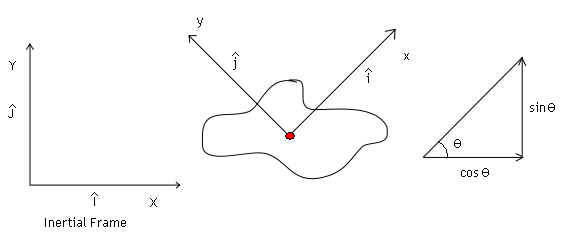
Thus unit vectors i and j are expressed in terms of unit vectors in the inertial reference frame, as

(14) i = cosθI + sinθJ

(15) i = − sinθI + cosθJ

Computing the derivatives of the unit vectors with time gives,

(16) (di)/(dt) = ( − sinθI + cosθJ)θ̇ = θ̇j = ωj

(17) (dj)/(dt) = ( − cosθI − sinθJ)θ̇ = − θ̇i = − ωi

Thus, moments about the center of mass can be expanded out as

(18) ΣM_c = I^c_xzω̇i + I^c_xzω(ωj) + I^c_yzω̇j + I^c_yzω( − ωi) + I^c_zzω̇k + I^c_zzω(0)

(19) ΣM_c = (I^c_xzα − I^c_yzω²) i ← M_cx + (I^c_yzα − I^c_yzω²) j ← M_cy + I^c_zzαk ← M_cz

If motion is restricted to a plane then, net force is also zero. Consider first the case where there are symmetric planar bodies.

(20) I_xz = I_yz = 0 ⇒ M_cx = M_cy = 0

The body’s motion is governed by:

(21) M_cz = I^c_zzα = I^c_zzθ̈

This is clearly related to Euler’s equation with the moment of inertia replacing the mass. So for a 2D planar body (symmetric),

(22) ΣF_x = Σmẍ_c ΣF_y = Σmÿ_c ΣM_cz = I^c_zzθ̈

These equations are with respect to the inertial frame of reference.