Welcome to AE Resources

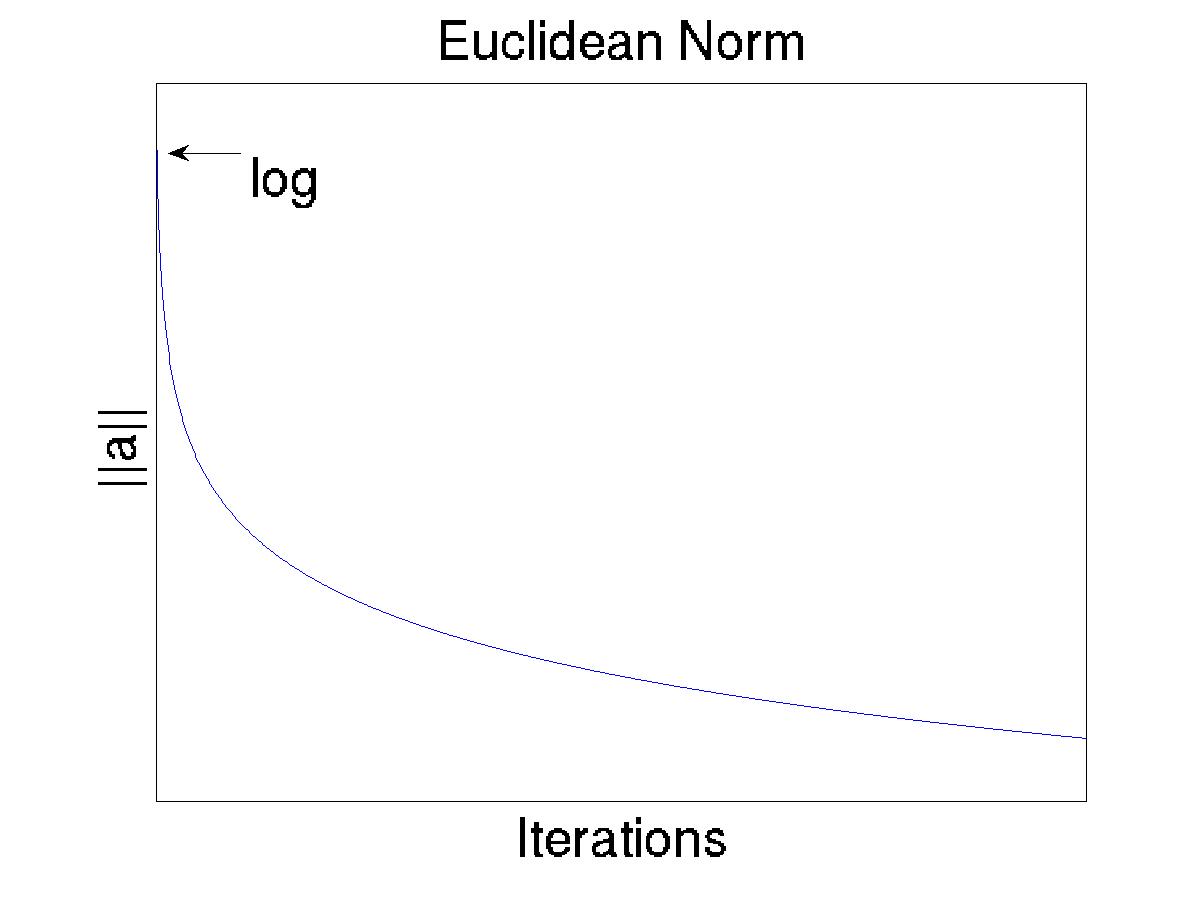
In an iterative simulation, the result should be approaching the final or exact value. Computing the norm at each iteration, should result in behavior similar to Fig. 1↓.

Figure 1 Illustration of the behavior of the Euclidean norm during an iterative solution.

In computations with matrices, one can compute the condition of the matrix. Condition(A) = ||A||*||A^− 1|| yields a measure of how reliable is the prediction error:

(||b||)/(||A||*||x||)*(||r||)/(||b||) ≤ (||e||)/(||x||) ≤ (||A^− 1||*||b||)/(||x||)*(||r||)/(||b||) (||b − Ax̂||)/(||b||) = (||x − x̂||)/(||x||)

In this computation, A^− 1 is needed, which can be a problem. A^− 1 can be estimated. If A is triangular, then the condition of (A) ≥ (||A||_∞)/(min|a_ii|). Otherwise,

(||x − x̂||)/(||x̂||) ≤ cond(A)(||E||)/(||A||)

where A = Â + E. If the cond(A) is large, then a small change in the matrix values will result in a large change. Therefore, the error will be large, as illustrated by

(1)/(cond(A)) = min⎧⎩(||A − B||)/(||A||)where B is not invertible⎫⎭ Bx = 0 x⃗ ≠ 0

A matrix is considered to be ill-conditioned if cond(A) is ’large’. In an engineering sense, this means that (1)/(u), where u is the roundoff error. Without knowing how conditioned a matrix is, one can get iterative improvement in the answer:

Ax = b x̂¹ is solution, e = x − x̂¹ r = b − Ax̂¹ x̂² = x̂¹ + ê¹ where Ae=r and ê is solution ...continue until... (||ê^k||)/(x̂^k) ≈ 10^− s

where s ≡ number of decimal places.

ERRORS AND NORMS