ROOT FINDING

ROOT FINDING

Engineers must numerically solve algebraic equations on a routine basis. This process is known as root finding. Usually the equation(s) to solve are recast (rewritten) so that the right hand side is zero. This is not always required, but it is typically the case.
There are various methods to obtain the roots of a single or a a set of equations. Some of the most popular include:
  1. Graphical method
  2. Bisection method
  3. Fixed-point iteration
  4. Newton-Raphson Iteration
The first two methods are considered Bracketing Methods, while the second two are Iterative Methods.

BRACKETING METHODS
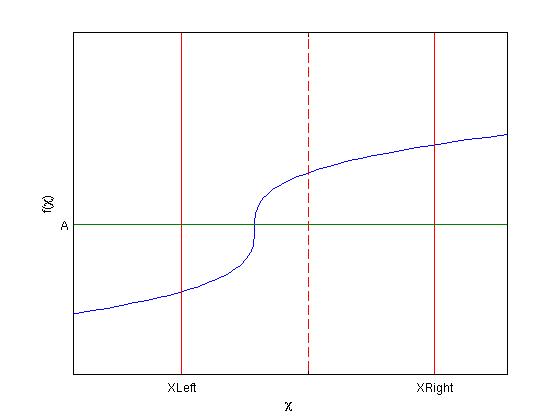
Bracketing methods are a way to find a root using upper and lower bounds. Graphically, the function is plotted and the location where the function value is zero (or a non-zero right hand side) is noted. The upper and lower limits of the plot abscissa act as the upper and lower brackets. This method is typically applied by hand, graphing calculator or excel. It requires visual inspection to locate the root.
There are several numerical bracketing methods, one of the most popular and easiest to program is the bisection method. The bisection method provides control of accuracy, but not round off errors, and a tolerance is typically needed. Underflows due to round off may be a problem as well. The root is rapidly found as the size of the search area is halved during each iteration. A pseudo-code example when the function is zero at the required location is given here:
figure images/Bisection_Method.jpg
Figure 1 Illustration of the bisection method.
f(x) = 0.0      Define xleft, xmid     If f(xleft)*f(xmid) < 0     xright replaced by xmid     If f(xmid)*f(xleft) > 0     xleft replaced by xmid     xm = 1 ⁄ 2(xleft + xright)     Loop over the if statements until xmis less than a preset tolerance      
ITERATIVE METHODS
Iterative methods are just what the name implies, the code iterates until it finds the answer. A bracketed method also iterates, but the difference here is that no upper and lower limit is needed.
Simple Fixed Point Method
The equation should be rewritten in terms of the unknown variable:
f(x)  =  x + 3ex = 0       x  =  3ex
For example, in the solution of the Prandtl-Meyer equation, the Mach number is the variable so that
M + ν(M)  =  f(M) + M       M  =  f(M) + M − ν(M)       M  =  g(M)
Given an initial guess, the solution will be updated until the solution approaches a single result:
initial guess is Mi  =  1.0       Mi + 1  =  g(Mi)        
Next Page →
Next Page →