Welcome to AE Resources

ROOT FINDING

Newton-Raphson Method

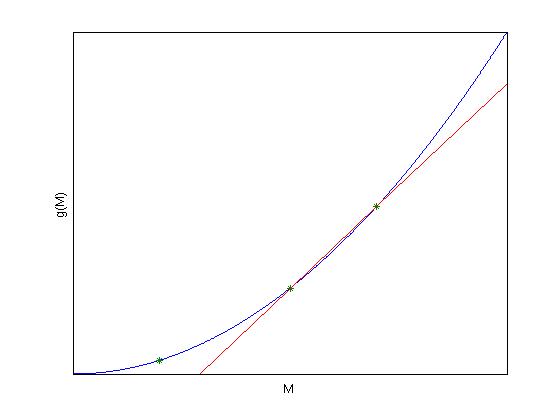
The Newton-Raphson method is an improved version of simple fixed-point method. This method works best if an analytical derivative of the function is known. This method first requires an initial guess for the function, after which the solution is found from the function (just as in the simple fixed point method) and the derivative of the function. This can be written mathematically as:

Initial guess M_i = 1.0 M_i + 1 = M₁ − (g(M₁))/(g’(M_i))

where g’(M_i) = (g(M_i − 1 − g(M_i))/(M_i − 1 − M_i). The process is illustrated graphically in Fig. 2↓. What happens when the derivative, g’(M_i), is not known?

Figure 2 Illustration of the secant or Newton-Raphson methods.

Multiple Roots

If a function has multiple roots (2 or more), then any of the methods can be modified to search the entire limits of interest for multiple roots. If the function has a tangent to zero, then it may not change sign, so a bracketing method may not work in all instances. The Newton-Raphson method can be modified for use with multiple roots:

x_i + 1 = x_i − (f(x_i)f’(x_i))/([f’(x_i)]² − f(x_i)f’’(x_i)) M_i + 1 = M_i − (g(m_i)g’(M_i))/([g’(M_i)]² − g(M_i)g’’(M_i))

Figure 3 Illustration of a function with multiple roots.

← Previous Page