Welcome to AE Resources

Convergence and Other Issues

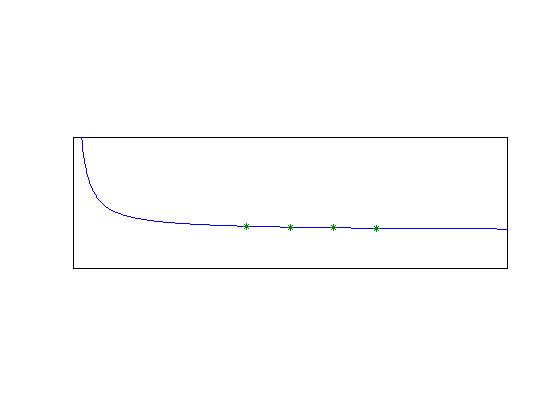
In the example provided, one can use tables of the Prandtl-Mayer expansion formula to check that the code has reached the correct location. What happens when that is not possible; how can one tell that the code has reached convergence without a known solution? The relative error concept from the the discussion of errors can be used to examine the solution behavior:

Error_rel = ||(M^new + Mold)/(M^new)||*100

This tracks the change in the estimate of the root. This is the concept of convergence, as illustrated in Fig. 4↓.. How fast these methods reach their solutions- want to maximize accuracy while minimizing time to get their solution. (operation count and iterations). To understand this, the concept of approximations is introduced.

Figure 4 Illustration of convergence.

Consider the derivative:

(dx)/(dt) ≈ (Δx)/(Δt) = (x(t_i + 1 − x(t_i))/(t_i + 1 − t_i)

If the function x is not linear with respect to time, then this is an approximation that can be estimated by a series:

f(x_i + 1) ≡ f(x_i) + f’(x_i)(x_i + 1 − x_i) + ... + (fⁿ(x_i))/(n!)(x_i + 1 − x_i)² + R_n ≡ f(x_i) [0^th-order approximation] ≡ f(x_i) + (∂f)/(∂x)Δx = f(x_i) + f’(x_i)(x_i + 1 − x_i) [2^ndorder approximation] R_n = (f^n + 1)/((n + 1)!)Δx^n + 1 [Remainder]

Using a Taylor Series to approximate the derivatives results for the first derivative and a first-order remainder will result in:

f(x_i + 1) = f(x_i) + f’(x_i)Δx = + R_n f’(x_i) = (f(x_i + 1) − f(x_i))/(Δx) + (R_n)/(Δx) R_n = (f)/(2)Δx² (R_n)/(Δx) = (f")/(2)Δx

ROOT FINDING