Welcome to AE Resources

Converted document

The permutation can be conducted because the averaging is done over a long period of time. Therefore, It can commute with the differentiation operator associated with another independent variable. Since U_j = U_j (already the average) and u_j’ = 0, the conservation of mass is reduced to

(11) (∂U_j)/(∂x_j) = 0

Conservation of momentum:

The Reynolds averaging process will be analyzed one term at a time. The unsteady term will only be non-zero for non-stationary turbulence.

(12) (∂u_i)/(∂t) = (1)/(T)^t + T⌠⌡_t(∂)/(∂t)(U_i + u_i’)dt = (U_i(x, t + T) − U_i(x, t))/(T) + (u_i’(x, t + T) − u_i’(x, t))/(T)

Providing that |u_i’|≪|U_i|, the second term can be neglected, so that

(13) (∂u_i)/(∂t)≃(∂U_i)/(∂t)

As mentioned by Wilcox [2], this aproximation is highly questionable. The turbulent fluctuations are typically not negligible compared to the mean flow. In some cases, fluctuations account for more than 10% of the mean value (see theory section on the Boussinesq assumption). Despite its admitted defficiencies, this approximation remains useful for analyzing non-stationary turbulence. The viscous and pressure terms can also be averaged similarly to the continuity equation.

(14) ν(∂²u_i)/(∂x_j∂x_j) = ν(∂²U_i)/(∂x_j∂x_j) and − (1)/(ρ)(∂p)/(∂x_i) = − (1)/(ρ)(∂P)/(∂x_i)

Finally, the convective term is averaged.

(15) (∂)/(∂x_j)(u_iu_j) = (∂)/(∂x_j)(U_iU_j + U_iu_j’ + U_ju_i’ + u_i’u_j’)

with

(16) U_iU_j = U_iU_j ; U_iu_j’ = U_iu_j’ = 0 ; U_ju_i’ = U_ju_i’ = 0

so that

(17) (∂)/(∂x_j)(u_iu_j) = (∂)/(∂x_j)(U_iU_j + u_i’u_j’)

which leads to the Reynolds Averaged Navier-Stokes equations.

(18) (∂U_i)/(∂t) + (∂)/(∂x_j)(U_iU_j) = − (1)/(ρ)(∂P)/(∂x_i) + (∂)/(∂x_j)⎛⎝ν(∂U_i)/(∂x_j) − u_i’u_j’⎞⎠

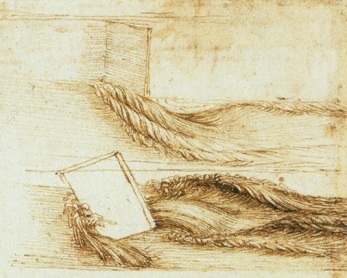
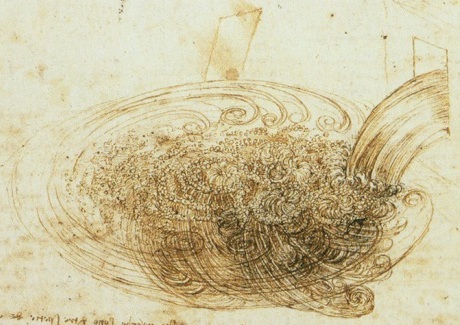
As an anectode, read the following statement written by Leonardo Da Vinci (translation by Ugo Piomelli, University of Maryland) around 1,500AD.

Observe the motion of the surface of the water, which resembles that of hair, which has two motions, of which one is caused by the weight of the hair, the other by the direction of the curls; thus the water has eddying motions, one part of which is due to the principal current, the other to random and reverse motion.

According to John Lumley [1], Da Vinci might have prefigured the Reynolds decomposition, well before the extensive analysis of Osborne Reynolds 400 years later!

Figure 1

Drawings of turbulent flows by Leonardo da Vinci ( ~ 1,500 AD).

References

[1] H. Tennekes and J.L. Lumley. First course in turbulence. MIT press, 1972.

[2] D.C. Wilcox. Turbulence modeling for CFD, volume 3. DCW industries La Cañada, 2006.