Welcome to AE Resources

Flutter is a dynamic instability that an aircraft may encounter due to an interaction of aerodynamic, inertial, and elastic forces. Lifting bodies such as wings, tails, and control surfaces may be subject to large aerodynamic loading resulting in flutter. A possible consequence of this phenomenon is structural failure. Therefore, all such lifting surfaces on any aircraft are subject to analysis and tests to ensure that flutter will not occur during the flight envelope. A special case of flutter, known as stall flutter, occurs on rotating lifting bodies such as in rotor blades or compressors caused by separation of the flow on the blades. Stall flutter makes the governing equations nonlinear.

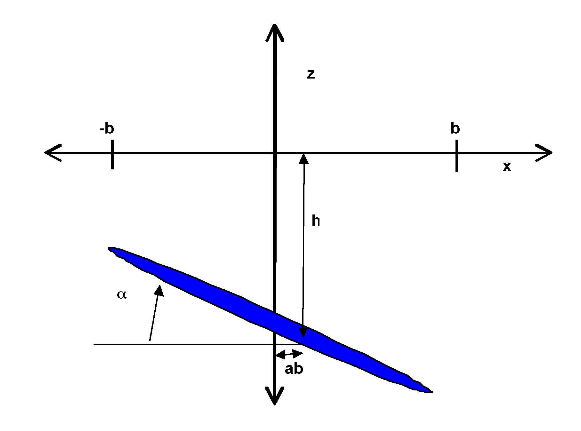
Two-Degree-of-Freedom Flutter

Figure 1 Schematic of an airfoil undergoing pitching and plunging. Pitching occurs at x = ab.

The equations of motion for this system are

(1) m(ḧ + bx_αα̈) + k_hh = − L I_Pα̈ + mbx_α + k_αα = M

where I_P is the moment of inertia about the point of pitching. Also, noting that M_1 ⁄ 4 is the moment about the quarter chord,

(2) M = M_1 ⁄ 4 + b⎛⎝(1)/(2) + a⎞⎠L

Presuming that the motion is simple harmonic (h = he^iωt and α = αe^iωt), the lift and moment is

(3) L = Le^iωt M = Me^iωt

The airloads are assumed to be complex, linear functions of the amplitudes of motion

(4) L = − πρ_∞b³ω²⎡⎣l_h(k, M_∞)(h)/(b) + l_α(k, M_∞)α⎤⎦ M = πρ_∞b⁴ω²⎡⎣m_h(k, M_∞)(h)/(b) + m_α(k, M_∞)α⎤⎦

where the reduced frequency is k = (bω)/(U) and M is the Mach number.

substituting the time-dependent functions into the equations of motion yields the following pair of equations for h and α

(5) − ω²mh − ω²mbx_αα + mω²_hh = − L − ω²mbx_αh − ω²I_Pα + I_Pω²_αα = M.

Combining the above expressions yields a pair of homogeneous relations for h and α

(6) ⎡⎣μ⎛⎝1 − ⎛⎝(ω_h)/(ω)⎞⎠²⎞⎠ + l_h⎤⎦(h)/(b) + (μx_α + l_α)α = 0 (μx_α + m_h)(h)/(b) + ⎡⎣μr²⎛⎝1 − ⎛⎝(ω_α)/(ω)⎞⎠²⎞⎠ + m_α⎤⎦α = 0

where

(7) μ = (m)/(πρ_∞b²) r = √((I_P)/(mb²)).

FLUTTER