ACCELERATION

To consider acceleration, we need to differentiate the velocity equation that we obtained. Recall that the velocity equation is:

Differentiating the equation:

Several of the quantities to be differentiated are already in the F frame. They will become their acceleration values by definition.

For the two derivative terms that do not have definition explicitly within frame F, we can apply the derivative formula:

and

Substituting back into our acceleration equation gives:

Let us rearrange the terms:

(A)

Let us examine the terms that are underlined:

Consider a point coincident with our point P, but moving with the original motion of the airplane. We shall call this point P_B to distinguish it from P.

The velocity equation is written as:

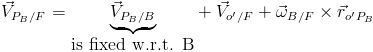
Taking the derivative yields:

Since , we can write

.

This is the equation that defines the acceleration of a point within a moving frame w.r.t. the fixed frame. We also see that the terms on the right hand side (RHS) of this equation are the underlined terms in Eqn. (A). So, we can write

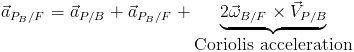
The coriolis term negates the additive theorem for acceleration a just as the additive ω×ω terms negated the additive theorem for angular acceleration α.

Again, in Aerospace Engineering this expression is used with a slightly different terminology: