|
||||||||
 |
 |
 |
 |
|||||
 |
||||||||
 |
||||||||
 |
 |
|||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
EXAMPLES OF CONSTRAINTS
BASIC MOTION CONSTRAINTS
These constraints simply specify that there is no translation or rotation about certain axes. As a result, when deriving the equations of motion for a system, the equations in these directions can simply be ignored, and it is understood that there are no degrees of freedom in these directions. Many simple problems implicitly include these constraints. For example, it is very common for problems to only include translation in one or two axes and either no rotation or rotation about one axis only.
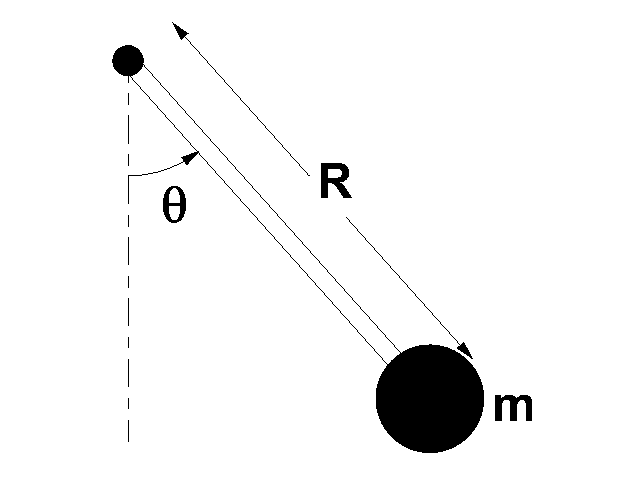
PENDULUM: RADIAL CONSTRAINT
Figure 1↑ shows an example of another constraint. This problem shows a simple pendulum swinging in the x − y plane. The position of mass m could be described by the coordinates x and y, but there is a radial constraint because the length of the pendulum is fixed. Mathematically, this constraint is x2 + y2 = R2. Therefore, when writing the equations of motion for the system, one of x or y could be substituted by this constraint. After the substitution, there will be only one dependent variable in the system, which is consistent with the number of degrees of freedom.
As an alternative to using x or y, it may be more convenient to use θ as the generalized coordinate. No matter which variables are used to describe the motion of the mass, there must be just one generalized coordinate because the radial constraint reduced the number of degrees of freedom from two to one.
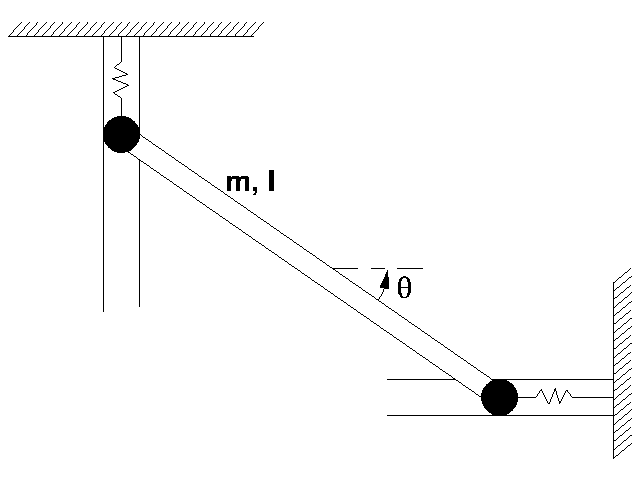
CONSTRAINT ON DIRECTION
In Fig. 2↑, the center of mass may again move in the plane x − y plane. The rigid body may also rotate about the z-axis (out of the page). However, there are two constraints on the motion, so the number of degrees of freedom is reduced from three to one. In this example, the left end is constrained so that it may only move in the y-direction (vertically), and the right end is constrained so that it may only move in the x-direction (horizontally). As in the previous example, since there is one degree of freedom, one generalized coordinate is required to describe the motion of the rigid body. A logical choice would be the angle θ, but one could also use the vertical position of the left end, the horizontal position of the right end, or a variety of other choices.
Next Page →
Next Page →