GENERALIZED COORDINATES

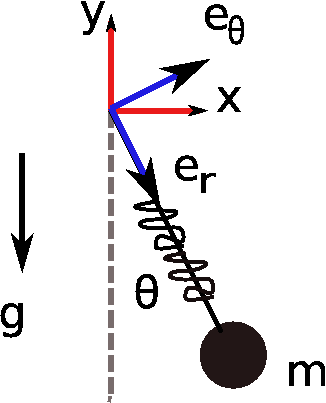
Figure 1↑ shows a pendulum with two degrees of freedom. This system can be fully described by the deflection of the spring, r, and the angle θ, so these two parameters make up a set of generalized coordinates for the system. An alternative set of generalized coordinates to describe the dynamics of this system is the set x and y in the cartesian system.

Note that, if the pendulum did not have a spring, then r would be fixed and only a single generalized coordinate would be needed (θ). Cartesian coordinates could still be used, but in that case only one of x or y is needed to uniquely define the position of the mass. The other cartesian coordinate would be related to the first by the constraint that x and y lie on a circular arc defined by r.

An additional example using generalized coordinates is available in Deriving Equations of Motion.