|
||||||||
 |
 |
 |
 |
|||||
 |
||||||||
 |
||||||||
 |
 |
|||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
DYNAMICS PROBLEMS
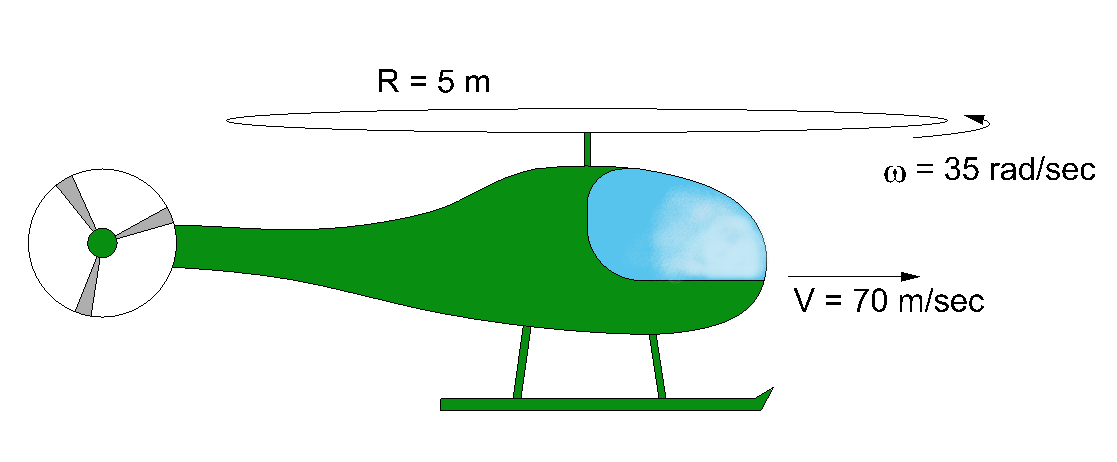
Example: Helicopter pull-up maneuver
The helicopter in Fig. 1↓ is flying at a speed of 70 m/sec, and its rotor speed is 35 rad/sec. The rotor radius, R, is 5 m. The helicopter is performing a pull-up maneuver with a radius, r, of 100 m.
Find:
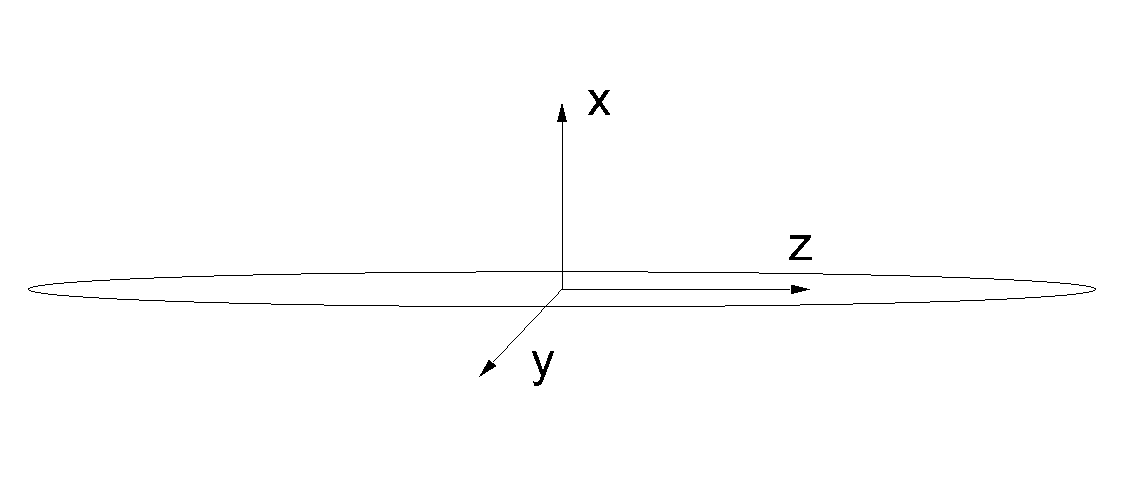
- The angular momentum of the rotor in the coordinate system shown in Fig. 2↓ which moves with the helicopter.
- The moment needed to be applied to the rotor to keep it from tilting during the maneuver.
Note: you may assume that the rotor disk may be approximated as a thin disk with mass m = 150 kg.
Solution
The first step is to find the moment of inertia of the rotor about each of the principle axes. For a thin disk with the coordinate system shown, the moment of inertia is:
(1)
Ix
= mR2 = 3750kgm2
Iy
= Iz = (1)/(2)mR2 = 1875kgm2
Next, the angular velocity about each axis is required.
(2)
ωx
= 35rad ⁄ sec
ωy
= (V)/(r) = 0.7rad ⁄ sec
ωz
= 0
1. It is now possible to find the angular momentum.
(3)
H
= Ixωxî + Iyωyĵ + Izωzk̂
= 3750⋅35î + 1875⋅0.7ĵ
= ⎡⎢⎢⎢⎣
131, 250
1312.5
0
⎤⎥⎥⎥⎦kgm2 ⁄ sec
2. To find the moment applied to the rotor, it is important to note that the coordinate system is rotating with constant angular velocity because the helicopter is executing a pull-up maneuver. The rotational velocity of the coordinate system, Ω, is