Welcome to AE Resources

Figure 1 Teeter-totter system with two masses

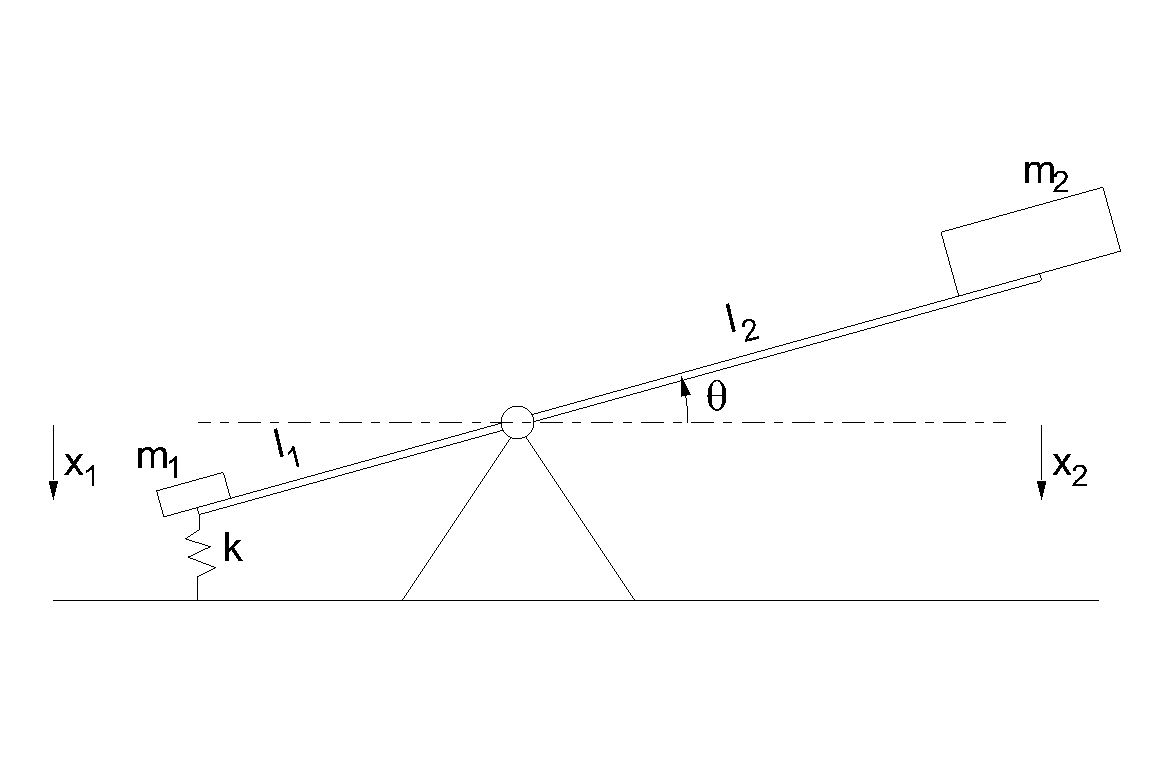
Problem: Use the principle of virtual work to determine the equilibrium equation for the system shown in Fig. 1↑.

Solution: There are two masses in the system. Consider the unit vector î to be pointing down in the figure and ĵ pointing to the right. The total forces acting on the two masses are:

(1) F₁ = (m₁g − kx₁)î F₂ = m₂gî

The positions of the masses m₁ and m₂ are

(2) σ₁ = x₁î + y₁ĵ σ₂ = x₂î + y₂ĵ

The virtual work done by the external forces is

(3) δW = ²⎲⎳_i = 1 F_i⋅δσ_i = (m₁g − kx₁)î⋅(δx₁î + δy₁ĵ) + m₂gî⋅(δx₂î + δy₂ĵ) = (m₁g − kx₁)δx₁ + m₂gδx₂

At this point, the coordinates x₁ and x₂ are written in terms of the angle θ:

(4) x₁ = l₁sinθ x₂ = − l₂sinθ

The virtual displacement δθ is the variation of θ, so the virtual displacements δx₁ and δx₂ can be written in terms of δθ by taking the variation of Eq. ↓.

(5) δx₁ = l₁cosθδθ δx₂ = − l₂cosθδθ

Substituting these expressions into the virtual work, the result is

(6) δW = (m₁g − kl₁sinθ)l₁cosθδθ − m₂gl₂cosθδθ

The principle of virtual work states that the virtual work done by all external forces in a system at equilibrium is zero, provided the virtual displacements are consistent with the constraints and that the constraint forces act perpendicular to the virtual displacements. Therefore, from the principle of virtual work, Eq. 6↑ becomes

(7) (m₁g − kl₁sinθ)l₁cosθδθ − m₂gl₂cosθδθ = 0

or

(8) [(m₁g − kl₁sinθ)l₁ − m₂gl₂]δθ = 0

However, since the virtual displacement δθ is arbitrary, the coefficient of δθ in Eq. 8↑ must vanish, so

(9) (m₁g − kl₁sinθ)l₁ − m₂gl₂ = 0

After some algebra, the equilibrium value of θ is determined:

(10) θ = sin^− 1⎡⎣(g)/(kl₁)⎛⎝m₁ − m₂(l₂)/(l₁)⎞⎠⎤⎦

VIRTUAL WORK EXAMPLE