Welcome to AE Resources

Converted document INERTIA PROPERTIES

INERTIA PROPERTIES

In terms of a three-dimensional body, the inertia properties refer to the nine components that make up the inertia matrix used in the calculation of angular momentum.

I = ⎡⎢⎢⎢⎣ I_xx I_xy I_xz I_yx I_yy I_yz I_zx I_zy I_zz ⎤⎥⎥⎥⎦

Each property is dependent on the geometry and mass of the body and is either referred to as a moment of inertia (I_xx, I_yy, I_zz) or a product of inertia (I_xy, I_xz, I_yx,I_yz, I_zx, I_zy).

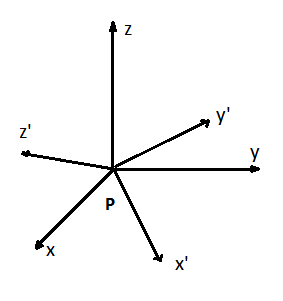
To change the reference frame of the inertia properties, defined by x, y, and z, to a different axis system, denoted by x’, y’, and z’, recall the parallel axis theorem:

(1) I^p_xx = I^c_x’x’ + m(y² + z²) I^p_xy = I^c_x’y’ − mxy

where I^c refers to the inertia property about point c, I^p refers to a different point p, and x, y and z, refer to the distances from point c to point p with respect to the axis defined for I^c.

Figure 1 Two reference frames (x,y,z and x’,y’,z’) with the same origin point P.

More specifically, the axes in the new reference frame can be related to the original reference frame through the angles between the the old and new azes. For instance, x’ can be defined as:

(2) x’ = (xi + yj + zk)⋅(l_xi + l_yj + l_zk)

where the variables l_x, l_y, and l_z are the direction cosines associated with the transform about x’. For instance, l_x is equal to the cosine of the angle between x’ and x, and the same concept applies for l_y and l_z. The dot product between the interia matrix and the vector of the directional cosines, or I⋅(l_xi + l_yj + l_zk), results in the following expression:

(3) I^p_x’x’ = l²_xI^P_xx + l²_yI^P_yy + l²_zI^P_zz + 2(l_xl_yI^P_xy + l_yl_zI^P_yz + l_zl_xI^P_zx)

For products of inertia, a similar equation can be used. Let η_x, η_y, and η_z be the direction cosines associated with the y’ axis. Given the definition of y’, similar to that of Equation 2↑:

(4) y’ = (xi + yj + zk)⋅(η_xi + η_yj + η_zk)

the inertial property I^p_x’y’ can be calculated as:

(5) I^p_x’y’ = l_xη_xI^P_xx + l_yη_yI^P_yy + l_zη_zI^P_zz + (l_xη_y + l_yη_x)I^P_xy + (l_yη_z + l_zη_y)I^P_yz + (l_zη_x + l_xη_z)I^P_zx

Therefore, if the inertial properties of the body in a fixed set of axes is known, then the inertial properties of P about any other axis system can be calculated.