Welcome to AE Resources
Converted document KINETIC ENERGY FOR AN INSTANTANEOUS CENTER

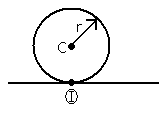
KINETIC ENERGY FOR AN INSTANTANEOUS CENTER

Find the kinetic energy for a rolling circular body, as seen in Figure 1↓.
figure images/InstantaneousCenter.png
Figure 1 Circular body of radius r with coordinate axes originating at center point C and an instantaneous center I.

For this case, where the velocity of the center VC is moving along one axial direction (VC = VCi for example), the kinetic energy is:
(1) KE  =  (1)/(2)mV2C + (1)/(2)ICω2        =  (1)/(2)m(ωd)2 + (1)/(2)ICω2        =  (1)/(2)(IC + md2)ω2        =  (1)/(2)IIω2
Here, II is the moment of inertia about point I or II = IC + md2 from the parallel axis theorem, where IC is the moment of inertia about point C, m is the mass of the body, and d is the distance from point C to point I.
Additionally, the velocity of the body’s center can be represented by the product of the body’s angular velocity and the distance from the center, point C, to the contact point to the ground, point I. The kinetic energy can be written as the following:
(2) KE  =  (1)/(2)mV2C + (1)/(2)ω2ICzz = (1)/(2)m(rω)2 + (1)/(2)ω2(mK2C)        =  (1)/(2)mω2(r2K2C)
where VC = rω and the moment of inertia is ICzz = mK2C or a product of the mass and radius of gyration. And thus for this case, equations 1↑ and 2↑ are equivalent:
(3) KE = (1)/(2)IIω2 = (1)/(2)mω2(r2K2C)
These calculations assume that the body MUST be rigid (the body does not deform or bend).