Welcome to AE Resources
Converted document MOMENTS OF INERTIA EXAMPLES

MOMENTS OF INERTIA EXAMPLES

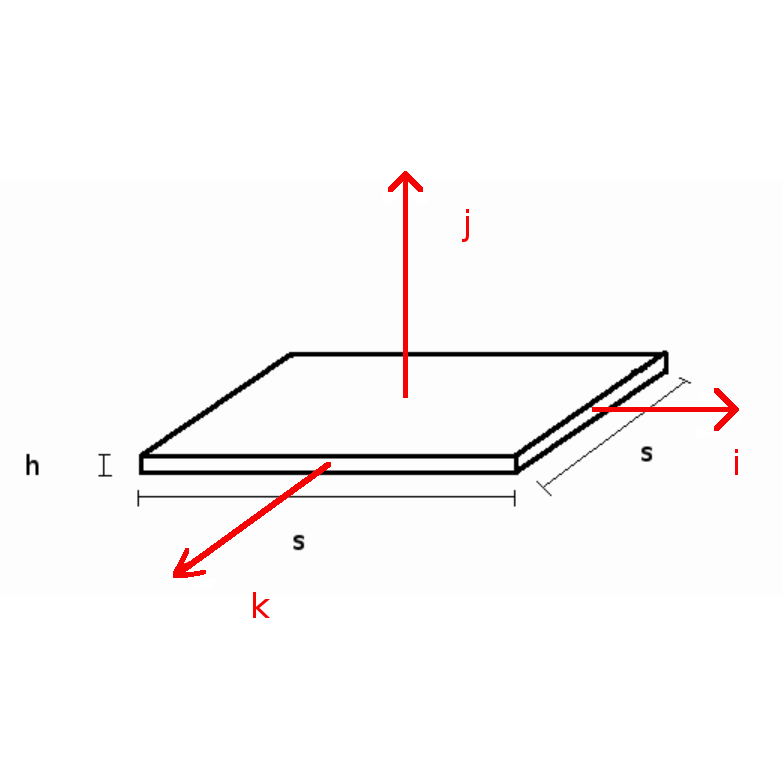
This example demonstrates how to compute the moment of inertia of a uniform square plate about the axis shown in the figure below. An example of how moments of inertia are used in solving engineering problems is given in the Deriving Equations of Motion section and Angular Momentum section.
figure images/plate.png
Figure 1 Square flat plate.
Consider a flat square plate of uniform material with mass m = 2 kg, thickness h = 0.1m, and length and width of s = 1m. Find the moments of inertia for this body given the axis system in Figure 1.

Answer: Ixx = 0.16833, Iyy = 0.16833, Izz = 0.33333

To get this answer, the equation for the moment of inertia is
(1) I =  ⌠⌡Vρr⋅rdV
where r is the vector that defines the location of an arbitrary point. In this case, Cartesian coordinates is the most convenient coordinate system to use for the geometry of this body, so r = xi + yj + zk. For the moment of inertia about the x axis (or x = 0), Equation 1↑ may then be rewritten as
(2) Ixx =  ⌠⌡Vρ(yj + zk)⋅(yj + zk)dV =  ⌠⌡Vρ(y2 + z2)dV
For a body with uniform material, the mass density ρ is constant, so it can be taken out of the integral. The limits of the integral are determined by the dimensions of the body. Given that the origin of the coordinate axes is located at the mass center, the result is
(3) Ixx = ρs ⁄ 2⌠⌡ − s ⁄ 2h ⁄ 2⌠⌡ − h ⁄ 2s ⁄ 2⌠⌡ − s ⁄ 2(y2 + z2)dxdydz
The function being integrated is an even function, that is f(x) = f( − x). Since for an even function, ∫a − af(x)dx = 2∫a0f(x)dx, so the evaluation of this integral can be simplified to
(4) Ixx = 2ρs ⁄ 2⌠⌡02h ⁄ 2⌠⌡02s ⁄ 2⌠⌡0(y2 + z2)dxdydz = 8ρs ⁄ 2⌠⌡0h ⁄ 2⌠⌡0s ⁄ 2⌠⌡0(y2 + z2)dxdydz
Evaluating the integrals:
(5) Ixx  =  8ρs ⁄ 2⌠⌡0h ⁄ 2⌠⌡0s ⁄ 2⌠⌡0(y2 + z2)dxdydz        =  8ρs ⁄ 2⌠⌡0h ⁄ 2⌠⌡0(s)/(2)(y2 + z2)dydz        =  8ρs ⁄ 2⌠⌡0(s)/(2)⎛⎝((h ⁄ 2)3)/(3) + z2(h)/(2)⎞⎠dz        =  8ρs ⁄ 2⌠⌡0(hs)/(4)⎛⎝((h ⁄ 2)2)/(3) + z2⎞⎠dz        =  8ρ(hs)/(4)⎛⎝((h ⁄ 2)2)/(3)(s)/(2) + ((s ⁄ 2)3)/(3)⎞⎠        =  8ρ(hs2)/(8)⎛⎝((h ⁄ 2)2)/(3) + ((s ⁄ 2)2)/(3)⎞⎠        =  (ρ(hs2))/(12)(h2 + s2)      
Next Page →
Next Page →