|
||||||||
 |
 |
 |
 |
|||||
 |
||||||||
 |
||||||||
 |
 |
|||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
THE DERIVATIVE
MEANING OF THE DERIVATIVE
The derivative of a function is a measure of the rate of change of a function’s value as the independent variable (the input) is changed. The simplest case to consider, which helps understand the concept, is the case of a straight line. For a straight line, the slope is a measure of how much the function value changes as the input changes, or
(1) m = (Δf(x))/(Δx)
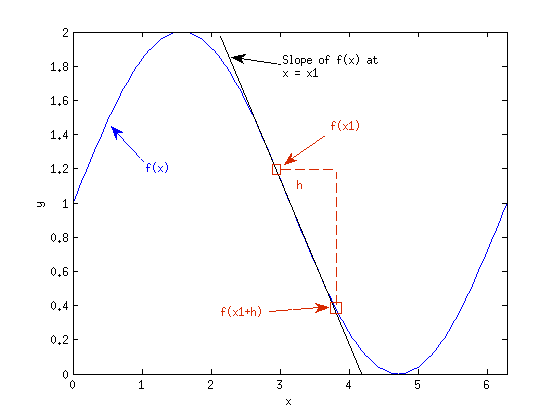
so the derivative of a straight line is equivalent to the slope of the line. In general, however, the derivative of a function is not constant but varies for different values of the input. For example, the derivative may have one value for x = 1 and a different value for x = 2. Nonetheless, the concept of the derivative as the slope is still meaningful if it is understood that for most functions, the slope changes from one point to the next. Consider Fig. 1↓ below, which shows a graph of the function f(x) = sinx + 1:
In this figure, the derivative is being sought at x = x1. The local slope of f(x) at this point is drawn; it is a line tangent to the function f(x) at x = x1. It is clear from this figure that the slope (and therefore the derivative) changes as the input x changes. If a tangent line were drawn at x = π ⁄ 2, the line would be horizontal, indicating that the derivative is 0 there. In Fig. 1↑, the derivative is initially large, but it decreases for 0 ≤ x < π. At x = π, the magnitude of the derivative is again relatively large, but it is negative. For π ≤ x < 2π the derivative increases again and at x = 2π it is once again equal to the derivative at x = 0. This cyclical nature of the derivative should not be surprising, considering the function itself is a sinusoidal function. It will be shown how to compute derivatives next.
DEFINITION OF THE DERIVATIVE
Mathematically, the concept of the slope is also useful. Consider again the function shown in Fig. 1↑. The slope of the function may be approximated at x1 by fitting a line between f(x1) and f(x1 + h), provided h is not too large. This approximation is valid because the slope of this fitted line is close to the slope of the line tangent to the function f(x) at x = x1. Therefore, we can approximate the derivative at x = x1 as
where f’(x1) is the derivative of f at x1. The reason why this expression is only an approximation of the derivative is because the line between f(x1) and f(x1 + h) is actually a secant line; it is not tangent to the curve at x1. However, the approximation could be improved by decreasing the value of h. If h is very small, then the approximation in Eq. 2↑ is very close to the actual derivative. It follows, then, that if h approaches 0, Eq. 2↑ approaches the derivative of f(x) at x1. Following this logic, the definition of the derivative is
The definition in Eq. 3↑ can be used to compute the derivative of a function at a given point.
Next Page →
Next Page →