Find the velocity of the diver at impact.
Assume constant acceleration due to gravity and neglect any friction forces.
v = ∫adt = ∫ − 9.8dt = − 9.8t + C1 m/s
Where C1 is the initial velocity. For this case, since the cliff diver had no velocity relative to the cliff before the jump, C1 = 0.0. Thus, the equation becomes
This can be integrated again to find the position of the diver at any time:
y = ∫vdt = ∫ − 9.8tdt = − (1)/(2)9.8t2 + C2 = − 4.9t2 + C2 m
Where C2 is the initial displacement. Since the cliff diver is initially standing 50 meters above sea level, C2 = 50 m.
Thus, the equation for the position is
Now that one has solved for the three equations of motion for this particular problem, the problem can be solved.
-
Since the cliff diver starts at an altitude of 50 meters and hits the water when y = 0, t can be solved directly from the equation for the position.. This will give the amount of time that it takes for the cliff diver to hit the water.
t = √((50)/(4.8)) = 3.23 sec
-
Now that the time it takes for the diver to hit the water is known, this time can be used in the velocity equation to solve for the velocity of the diver at impact (at y = 0m).
v = − 9.8(3.23) = − 31.65 m/s
The negative result is because the acceleration is defined as negative since it is in the opposite direction of the positive y direction, which is up. Conversely, the positive direction could be defined as down, and the value would be positive. Both are correct. It does not matter which direction is defined as positive as long as the problem uses these definitions consistently.














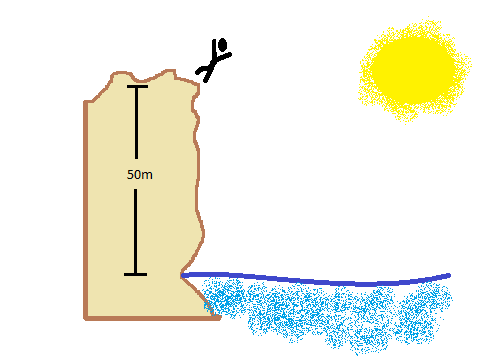 Begin by writing the equations of motion for this example:a = − 9.8 m/s2v = ∫adt = ∫ − 9.8dt = − 9.8t + C1 m/sWhere C1 is the initial velocity. For this case, since the cliff diver had no velocity relative to the cliff before the jump, C1 = 0.0. Thus, the equation becomesv = − 9.8t m/sThis can be integrated again to find the position of the diver at any time:y = ∫vdt = ∫ − 9.8tdt = − (1)/(2)9.8t2 + C2 = − 4.9t2 + C2 mWhere C2 is the initial displacement. Since the cliff diver is initially standing 50 meters above sea level, C2 = 50 m.Thus, the equation for the position isy = − 4.8t2 + 50 mNow that one has solved for the three equations of motion for this particular problem, the problem can be solved.
Begin by writing the equations of motion for this example:a = − 9.8 m/s2v = ∫adt = ∫ − 9.8dt = − 9.8t + C1 m/sWhere C1 is the initial velocity. For this case, since the cliff diver had no velocity relative to the cliff before the jump, C1 = 0.0. Thus, the equation becomesv = − 9.8t m/sThis can be integrated again to find the position of the diver at any time:y = ∫vdt = ∫ − 9.8tdt = − (1)/(2)9.8t2 + C2 = − 4.9t2 + C2 mWhere C2 is the initial displacement. Since the cliff diver is initially standing 50 meters above sea level, C2 = 50 m.Thus, the equation for the position isy = − 4.8t2 + 50 mNow that one has solved for the three equations of motion for this particular problem, the problem can be solved.