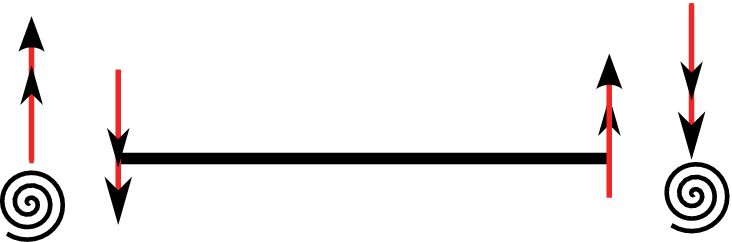Welcome to AE Resources
EXAMPLES: BOUNDARY CONDITIONS FOR BEAMS IN BENDING
Prescribed displacement
Figure 4↓ shows a special case. Root of this beam has a prescribed displacement w = a0sin(ωt) and the other end has a clamped boundary condition.
(5) x = 0 : w = a0sin(ωt) θ = 0       x = l : w = 0 M = 0
with the Euler-Bernoulli assumption:
(6) x = 0 : w = a0sin(ωt) θ = 0       x = l : w = 0 θ = (∂w)/(∂x) = 0
figure images/prescribedd.png
Figure 4 Prescribed displacement-clamped beam

Translational spring reinforcement
Figure 5↓ shows a beam that is reinforced with a translational spring at each end. Figure 6↓ shows action and reaction force on springs and beam. Considering conventional positive sign for shear force at each end of the beam, one can write the boundary conditions as below
figure images/transpring.png
Figure 5 Spring reinforced beam

figure images/transpringFB.png
Figure 6 Action and reaction force on springs and beam

(7) x = 0 : M = 0 F = kw       x = l : M = 0 F =  − kw
with the Euler-Bernoulli assumption:
(8) x = 0 : M = 0 F =  − (∂)/(∂x)⎛⎝EI(∂2w)/(∂x2)⎞⎠ = kwx = 0       x = l : M = 0 F =  − (∂)/(∂x)⎛⎝EI(∂2w)/(∂x2)⎞⎠ =  − kwx = l
Next Page →
Next Page →
← Previous Page
← Previous Page