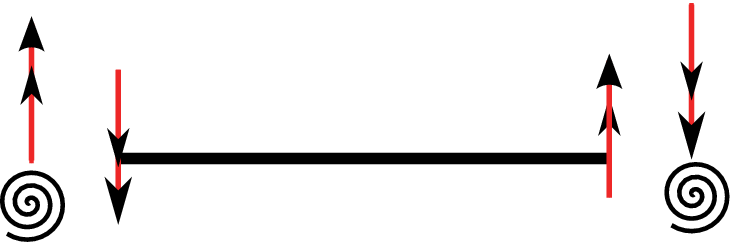Welcome to AE Resources

EXAMPLES: BOUNDARY CONDITIONS FOR BEAMS IN BENDING

Rotational spring reinforcement

Figure 7↓ shows a beam that is reinforced with rotational spring at each end. Figure 8↓ shows action and reaction moment s on springs and beam. One can write the boundary conditions as below

Figure 7 Spring reinforced beam (rotational)

Figure 8 Action and reaction force on springs and beam (rotational)

(9) x = 0 : F = 0 M = kθ x = l : F = 0 M = − kθ

with the Euler-Bernoulli assumption:

(10) x = 0 : F = 0 M = EI(∂²w)/(∂x²) = k(∂w)/(∂x)_x = 0 x = l : F = 0 M = EI(∂²w)/(∂x²) = − k(∂w)/(∂x)_x = l

Point mass at each end

Figure 9↓ shows a beam with point mass at each end. Figure 10↓ shows action and reaction force on point mass and beam. One can write the boundary conditions as below

Figure 9 Beam with a point mass at each end

Figure 10 Action and reaction force on point masses and beam

(11) x = 0 : M = 0 F = μ(∂²w)/(∂t²) x = l : M = 0 F = − μ(∂²w)/(∂t²)

with the Euler-Bernoulli assumption:

(12) x = 0 : M = EI(∂²w)/(∂x²) = 0 F = − (∂)/(∂x)⎛⎝EI(∂²w)/(∂x²)⎞⎠ = μ(∂²w)/(∂t²)_x = 0 x = l : M = EI(∂²w)/(∂x²) = 0 F = (∂)/(∂x)⎛⎝EI(∂²w)/(∂x²)⎞⎠ = μ(∂²w)/(∂t²)_x = l

← Previous Page