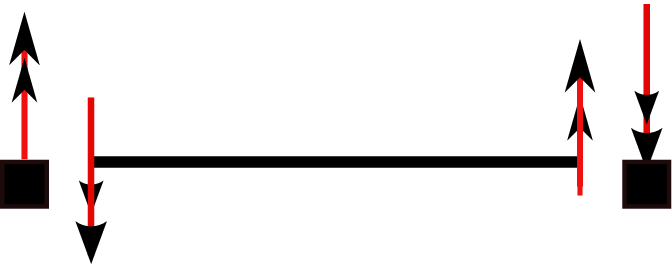Figure 11↓ shows a beam with rigid body mass at each end. A rigid body mass will effect the boundary condition on shear for the same as point mass, so we avoid repeating it here again. At same time, a rigid body effects boundary condition on moment due to non-zero moment of inertia. Figure 12↓ shows action and reaction moment on rigid body mass and beam. One can write moment equilibrium equation for rigid bodies and boundary conditions as below

where α_m is the angular acceleration of the rigid body equal to (∂³w)/(∂x∂t²) and

with the Euler-Bernoulli assumption: