Welcome to AE Resources
Converted document Beam Bending Dynamics

Beam Bending Dynamics

Equation of Motion
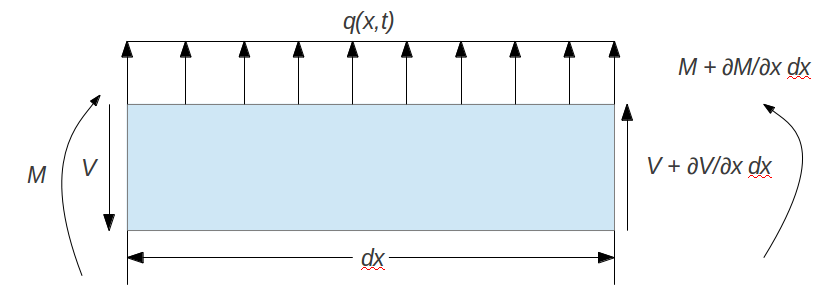
figure images/diffBeam.png
Figure 1 Differential beam segment

Starting with the free body diagram in Fig. 1↑, the forces on the beam segment can be added and equated to its mass multipled by its acceleration (Newton's 2nd Law):
(1) q(x, t)dx − V + ⎛⎝V + (∂V)/(∂x)dx⎞⎠ = mdx(∂2w)/(∂t2)
resulting in
(2)  − (∂V)/(∂x) + m(∂2w)/(∂t2) = q(x, t).
Similarly for the moment equation the following balance is obtained:
(3)  − M + ⎛⎝M + (∂M)/(∂x)dx⎞⎠ + ⎛⎝V + (∂V)/(∂x)dx⎞⎠ − (1)/(2)m(∂2w)/(∂t2)dx2 = 0
leading to
(4)  − (∂M)/(∂x) + V = 0.
Since bending moment is proportional to local curvature, one can substitute M = EI(∂2w)/(∂x2) into Eq. 4↑ and the resulting equation into Eq. 2↑ to obtain
(5) EI(∂4w)/(∂x4) + m(∂2w)/(∂t2) = q(x, t)
for a uniform beam.
If one considers free vibration (no distributed load), q(x, t) = 0 and introducing a parameter β such that β4 = (EI)/(m), the equation of motion results in
(6) β4(∂4w)/(∂x4) + (∂2w)/(∂t2) = 0
Next Page →
Next Page →