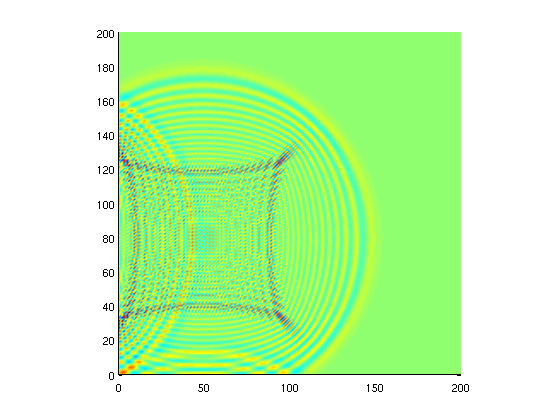
Wave Equation Demo

This demo simulates a stone striking a calm pond. It also allows one to see how the 2-D wave equation can be solved using a finite difference approach. It requires matlab to run (the matlab .m files are stored: here).

This demo shows the effects of reflections by visually illustrating them. To try it, extract the matlab files and run the “main” code.

The code is very flexible and allows for many different options. The location the stone is thrown into the pond may be changed by adjusting the initial conditions (domain.u(x,y)=domain.u0(x,y)  > 0). The size of the domain may be changed by adjusting domain.Lx (width) and domain.Ly (length). The simulation grid can be refined by decreasing domain.dx (along with the timestep domain.dt) for more accurate simulations or coarsened (by increasing domain.dx) to reduce computational cost. The speed of sound inside the domain is adjusted by changing domain.C. To run the simulation out longer, increase “timesteps”. To visualize more solutions increase “savesteps”.

The simulation has an interesting option of “turning off” the reflections by setting “reflect = false”. Can you figure out how this works? Hint: Examine how the traveling wave solution can be split into left and right waves in 1D!