Consider a rigid model of a uniform wing that stretches across the entire width of a wind tunnel. It pivots about the mid-chord and is elastically restrained in pitch by a torsional spring with a linear spring constant of 50 lb-in/rad. The model consists of a NACA0006 airfoil, and it has a span of 2 ft and a chord of 4 in. Assume that the aerodynamic center is at the quarter chord of the airfoil, and the center of gravity is at the mid-chord. How does altitude influence the divergence speed?

The first step is to draw the free body diagram of the problem:

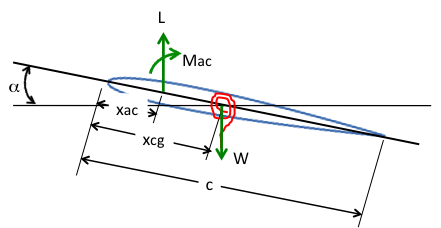
Since there is only one degree of freedom (torsion), only the summation of moments is necessary. Here, the location of the center of gravity x_cg is also the pivot point where the spring is located x_o. It is best to write out equations of motion using symbols before substituting numbers as it is easier to track down errors.

Since the airfoil is symmetric, M_ac = 0. The lift, L, is nonzero, but it depends on the angle of attack. The angle of attack is defined as α = α_rigid + θ. Using small angle approximations, which implies that the airfoil behavior will remain in the linear range. If the airfoil remains in the linear range, the lift per unit span will respond based on the following equation: L’ = (∂c_ℓ)/(∂α)q_∞cα. Since the airfoil spans the entire wind tunnel, it is known as a semi-infinite wing, and the lift per unit span is the same across the wing. Thus, the lift per unit span can be multiplied by the span (b) to provide the entire lift of the model: L = (∂c_ℓ)/(∂α)q_∞cbα = (∂c_ℓ)/(∂α)q_∞Sα, where S is the planform area (S = bc).

The equation of motion now becomes

The unknown in the equation is θ, so rearranging the equation to put the unknown on the left side results in

Divergence will occur in theory when θ → ∞. Looking at the right hand side, this occurs when the denominator approaches zero:

The unknown now is the dynamic pressure at which the aerodynamic loads will overcome the ability of the structural model to maintain the torsional response to small values. Rearranging the equation for this yields

The lift curve slope of the NACA0006 airfoil is (∂c_ℓ)/(∂α) = 0.11 ⁄ ^○ = 6.30 ⁄ rad. The thin airfoil lift curve slope (2π) should not be used unless there is no specific airfoil data available. Now substitution of the numbers yields (with units of feet)

The dynamic pressure is defined at 0.5ρV², where ρ is the air density and V is the velocity of the tunnel. The dynamic pressure for divergence is constant, so the velocity will change with the square root of the inverse of the density. As altitude increases, so will the speed at which divergence will occur.