Welcome to AE Resources
Converted document Converted document

SMALL ANGLE APPROXIMATIONS

The small angle approximations have been identified as being useful tools, but how accurate are they?
Consider a simple frame transformation from cylindrical to Cartesian coordinates
(1) i  =  cos(θ)er − sin(θ)eθ       j  =  sin(θ)er + cos(θ)eθ       k  =  k
If the small angle approximation is applied, then these equations become
(2) i  =  1.0er − θeθ       j  =  θer + 1.0eθ       k  =  k
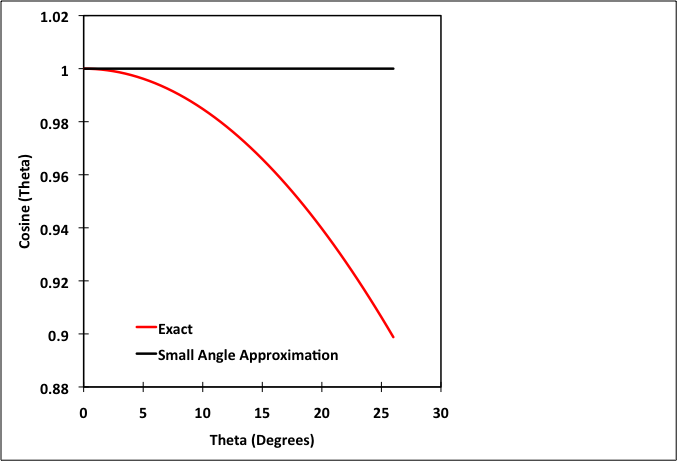
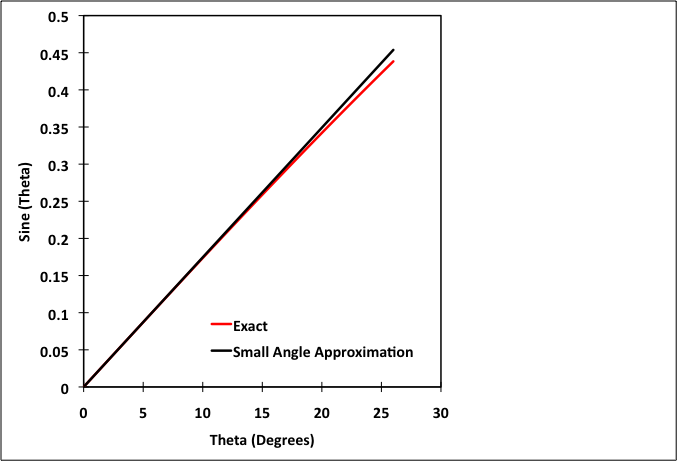
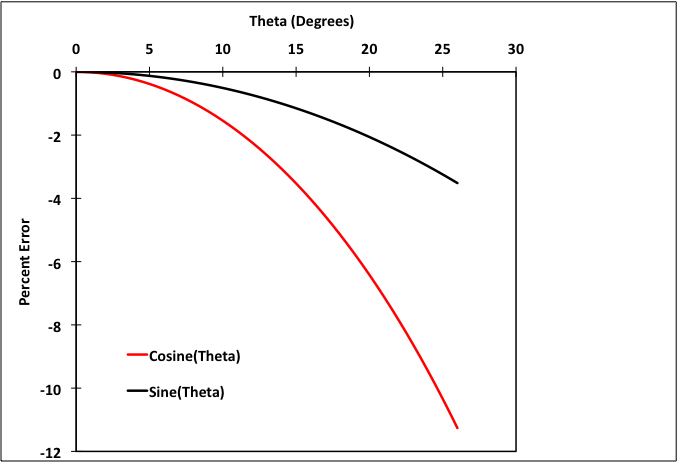
θ should be applied in radians in these equations. Observe the behavior of the approximation as θ increases in Fig. 1↓. It is clear that the cosine approximation generates more error as θ increases than its sine counterpart. The errors ((exact - approximation)/exact  × 100%) are shown in Fig. 2↓.
figure images/cos.png figure images/sin.png
Figure 1 Small angle approximations for sin(θ) and cos(θ).
figure images/error.png
Figure 2 Small angle approximation errors for sin(θ) and cos(θ).

For an engineering tolerance of 4%, the angle θ can go to 25° if only sine functions are modeled, but the error exceeds the tolerance at 15° if cosine functions are approximated. For smaller tolerances, the largest “small” angle reduces.