Welcome to AE Resources

Converted document

STATIC EQUILIBRIUM>

Example 1

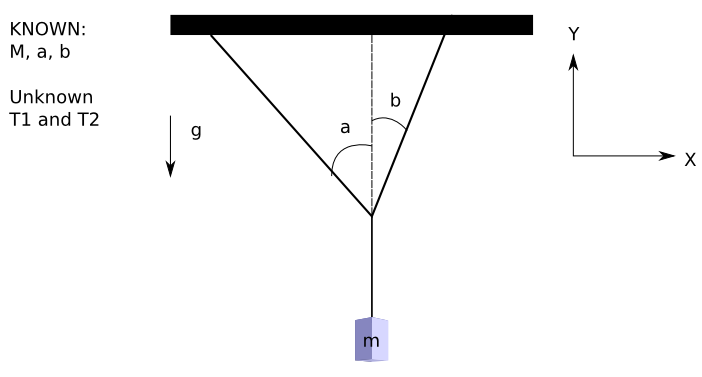
Consider the following example of a box that is hanging from two cables (see Fig. 1↓). Since it is in static equilibrium, it is not moving or rotating. In order for this to occur the net forces and moments in each coordinate direction must equal zero. For simplification, this problem has no applied moments.

Figure 1 A box hanging from two cables.

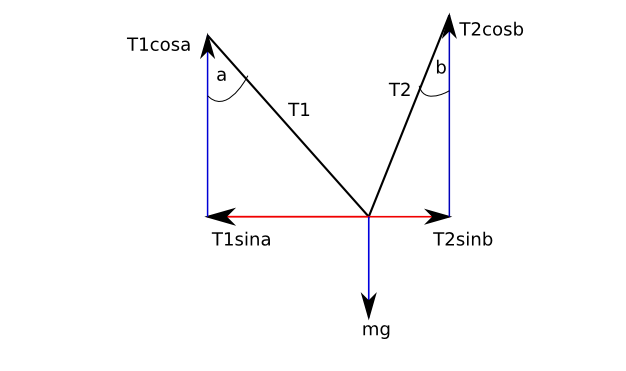
After selection of the Cartesian coordinate system, the forces on the box are identified, and these forces are decomposed into their x and y components as shown in Fig. 2↓.

Figure 2 Free body diagram for example 1.

Next, the equations of equilibrium are written:

ΣF_x = 0

− T₁sina + T₂sinb = 0

ΣF_y = 0

T₁cosa + T₂cosb − mg = 0

There are two equations for the two unknowns, thus, this problem can be solved without further information. Solve for T₁ or T₂ from ΣF_x = 0:

T₁ = (T₂sinb)/(sina)

Replace T₁ into the ΣF_y = 0 equation:

T₁cosa + T₂cosb − mg = 0
(T₂sinb)/(sina)cosa + T₂cosb = mg
T₂⎛⎝(sinb)/(tana) + cosb⎞⎠ = mg

T₂ = (mg)/(⎛⎝(sinb)/(tana) + cosb⎞⎠)

Substitute T₂ into the previous expression for T₁ (that is a function of T₂).