Welcome to AE Resources
Converted document INTRODUCTION TO BEAM THEORY

INTRODUCTION TO BEAM THEORY

Beams are slender structures in which one dimension is much larger than the other two dimensions. One can model beam-like structures as a two dimensional problem over the cross-section and a one dimensional problem along the axis of the beam. This makes solving the problem much easier than solving the three dimensional elasticity problem. This write-up focuses on the one dimensional global problem.
This is a short write-up for undergraduate students on introduction to beam theory. For more information, see Papers.

EULER-BERNOULLI BEAM THEORY
Any structural problem requires three sets of equations.
Equilibrium equations  Newton’s second law must be satisfied in all levels in any dynamic or static problem including beam theory. Equilibrium equations are relationships between force and moments applied on the structure and resultant internal force and moments (stresses).
Kinematic formulation  is a set of equations that describes kinematic/geometry of the problem. This set of equations is a relationship between strain and displacement.
Constitutive law  is the out put of solving a two dimensional problem on cross section. One can get constitutive law from performing experiment. Constitutive law is a relation between, force/moment and strain measurements/curvature. This law relates the first two sets of equations (Equilibrium and kinematic formulation) together.
Different kinematic assumptions will result in different beam theories. Euler-Bernoulli and Timoshenko are two famous ones.

EULER-BERNOULLI BEAM THEORY
Here are the main kinematic assumptions:
  • The cross-section is infinitely rigid in its own plane.
  • The cross-section of a beam remains plane after deformation.
  • The cross-section remains normal to the deformed axis of the beam.
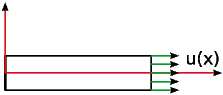
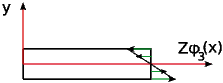
One needs to write these assumptions in a mathematical format to get kinematic formulation of the problem. Figure 1↓ shows a beam with the x axis along the slender dimension of the beam. Where the y--z plane makes the cross section. The displacement of each point along the x axis is u1(x, y, z), displacement of each point along the y axis is u2(x, y, z), and displacement of each point along the z axis is u3(x, y, z). The first Euler-Bernoulli assumption states that the cross-section is infinitely rigid in its own plane. Hence, the displacement field in the plane of the cross-section consists solely of two rigid body translations u2(x) and u3(x). Where ( ) is displacement of any point on the beam axis. If the cross-section is infinitely rigid in its own plane and remains plane after deformation, then Fig. 2↓ to 4↓ shows all the possibility of displacement for any point on the cross section. It can be either an axial displacement equal to displacement of the axis of the beam at the given x coordinate or rigid body motions due to rotation with angle φ2 or φ3. Therefore, one can write the displacement field as below:
figure images/beamtheory0x.png
Figure 1 Schematic of a beam
figure images/beamtheory1x.png
Figure 2 Schematic of a beam
figure images/beamtheory2x.png
Figure 3 Schematic of a beam
figure images/beamtheory3x.png
Figure 4 Schematic of a beam
(1) u1(x, y, z) = u1(x) + zφ2(x) − yφ3(x)     u2(x, y, z) = u2(x)     u3(x, y, z) = u3(x)
Next Page →
Next Page →