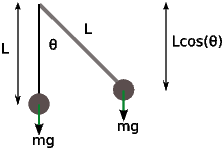
Substituting eqs. 5 and 6 into eqs. 1 and 2 and r = L, one can obtain the governing equation for pendulum.

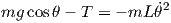(7)

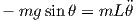(8)

Equation 8 is the one that governs the oscillation of the pendulum. Equation 7 can be used to calculate tension force T. One can simplify eq. 8 more.

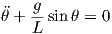(9)

For small θ one can approximate sinθ with θ so

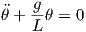(10)

Comparing eq. 10 with the basic one degree of freedom spring-mass vibration equation (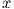 + ω_n²x = 0), natural frequency of pendulum is 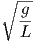. It is important to understand that natural frequency is not dependent on mass (m).

One of the characteristics of the Newtonian method in dynamics is that all the reaction forces and moments will appear in the equations of motions. For instance, in this example the tension force, T, appears in eq. 7. Sometimes it is helpful if one can get eq. 10 without having to consider, T. Analytical mechanics is a way for solving this problem. In next sections Lagrange’s method and Hamilton’s method are used to solve a simple pendulum problem.

LAGRANGE’S METHOD.

Lagrange’s formulation when there is no non-conservative force in the system is as follows

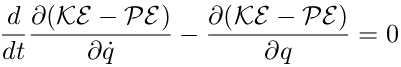(11)

Where KE is kinetic energy of the system, PE is potential energy of the system, q is the generalized degree of freedom and 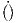is time derivative. For this example one can write the kinetic energy as below

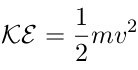(12)

where v is the velocity of mass m. Velocity of a mass particle in polar coordinates is

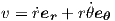(13)

Simplifying eq. 0.13 for pendulum problem by substituting r = L and ṙ = 0, one has

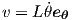(14)

Therefore, v² = L²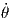² and

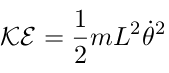(15)

Figure 3 shows that displacement of the center of mass as a function of θ is L(1 - cosθ).

Figure 3: Displacement of the center of mass

Therefore; the potential energy for this system is

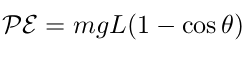(16)

One can derive each part of Lagrange’s equation (eq. 11) as follows

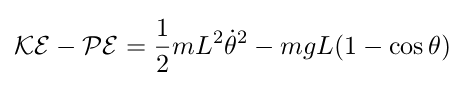(17)

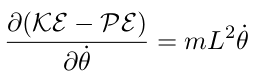(18)