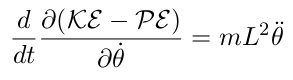Welcome to AE Resources
-d∂-(K---V-) 2¨ dt ∂ ˙θ = mL θ
(19)

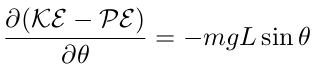∂(K---V-) ∂θ = - mgL sinθ
(20)

and finally
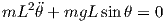mL2 ¨θ + mgL sinθ = 0
(21)

One can simplify eq. 21 to eq. 9. Notice that by using Lagrange’s method, one can avoid deriving a governing equation for tension force (T).

HAMILTON’S METHOD

When there is no non-conservative force and moments, one can write Hamilton’s principle as below
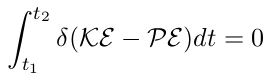∫ t2 δ(K - V )dt = 0 t1
(22)

Again KE is kinetic energy (eq. 15) and PE is potential energy (eq. 16); therefore, one can write
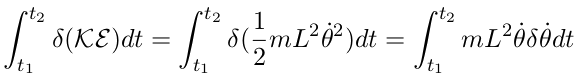∫ t2 ∫ t2 1 ∫ t2 δ(K )dt = δ(-mL2 ˙θ2)dt = mL2 θ˙δ˙θdt t1 t1 2 t1
(23)

Using integration by parts one can simplify eq. 23
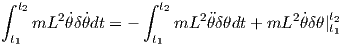∫ t2 2 ∫ t2 2 2 t mL ˙θδ˙θdt = - mL ¨θδθdt+ mL θ˙δθ|2t1 t1 t1
(24)

One can choose δθ such that the boundary terms in eq. 24 are zero (mL2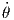˙θδθ|t1t2 = 0). Hence
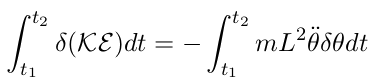∫ t2 ∫ t2 2 δ(K )dt = - mL ¨θδθdt t1 t1
(25)

One can also simplify the term related to potential energy in Hamilton’s principle as below
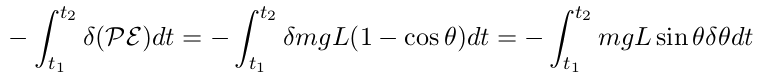∫ t ∫ t ∫ t - 2 δVdt = - 2δmgL (1- cos θ)dt = - 2mgL sin θδθdt t1 t1 t1
(26)

Substituting eqs. 25 and 26 into eq. 22 one has
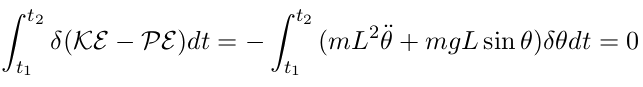∫ t2 ∫ t2 δ(K - V)dt = - (mL2 ¨θ + mgL sin θ)δθdt = 0 t1 t1
(27)

In eq. 27, δθ is arbitrary so for the eq. 27 to hold, mL2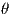θ + mgLsinθ = 0,which is the same as eq. 21.

PRINCIPLE OF CONSERVATION OF ENERGY

Since there is no source or sink of energy, the principle of conservation of mechanical energy holds.
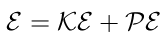E = K + V = cte
(28)

Where E is mechanical energy. One can write eq. 28 between two difference points along motion of mass, point A and B.
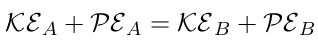K + V = K + V A A B B
(29)

EASY EXPERIENCE

← Previous Page
← Previous Page