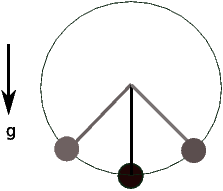
2-D PENDULUM

A simple pendulum is made of a mass attached to a rigid bar in gravity field (Figure 1). To derive the simplest form of governing equations this problem, one needs to make several assumptions, such as absence of any damping source and planar motion.

FORMULATION

There is no source of energy dissipation like friction in deriving of these equations at this point. This is only a simplified assumption. One can derive the governing equation of this pendulum with different methods. Here, several of them are reviewed.

EQUILIBRIUM (NEWTONIAN) METHOD

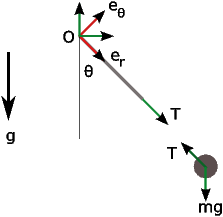
The first step in solving a dynamics problem with the Newtonian method is to specify a frame of reference. For this problem, a polar frame of reference with origin at the point O is a suitable frame. Mass is assumed to be a point mass in the problem. This is another simplifying assumption. The second step is to draw free body diagram for each body (Figure 2).

The third step is to write equilibrium equations for each body. The body of interest here is the mass. This is a planar problem; therefore, there are three equilibrium equations. Since mass is assumed to be a point mass, moment equilibrium will not provide any information. The two force equilibrium equations are as shown below

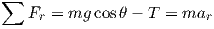(1)

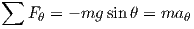(2)

a_r and a_θ are acceleration in e_r and e_θ direction. One can find them from kinematics of the problem. These accelerations are written relative to a polar coordinate system.

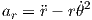(3)

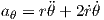(4)

For this problem r is constant, since the rod is assumed to be rigid (r = L); therefore, ṙ = 0 and 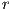= 0. Equations 3 and 4 are simplified to the following equations.

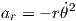(5)

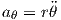(6)