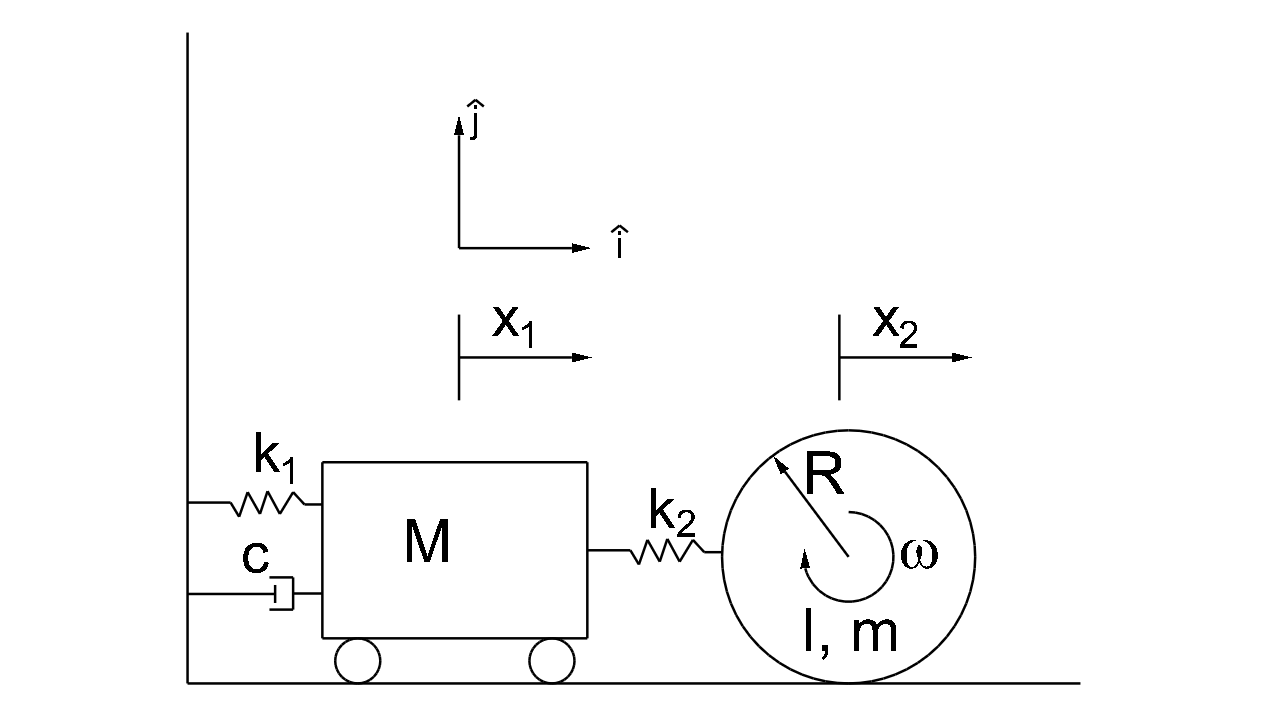
Consider the system in Fig. 1↓. The system has two masses, one with mass M and the other with mass m and moment of inertia I about the k̂-axis (out of the plane). Both masses may translate, but the second mass also rolls as it translates. Assume no slipping occurs, and that the motion of mass 1 in the horizontal direction is frictionless. The two masses are connected to each other and the wall by the springs and dampers shown, and there is no motion in the vertical direction or the direction into the plane. The goal is to develop the equations of motion governing the dynamics of the system, using both the Newtonian method and Lagrange’s method.

There are two bodies in the system; n = 2. There are six degrees of freedom per body, so m = 12. The constraints are as follows:

Body2

In total, there are ten constraints; l = 10. The number of unconstrained degrees of freedom is N = m − l = 2. This is also the number of generalized coordinates. As defined in Fig. 1↑, x₁ and x₂ are the generalized variables.

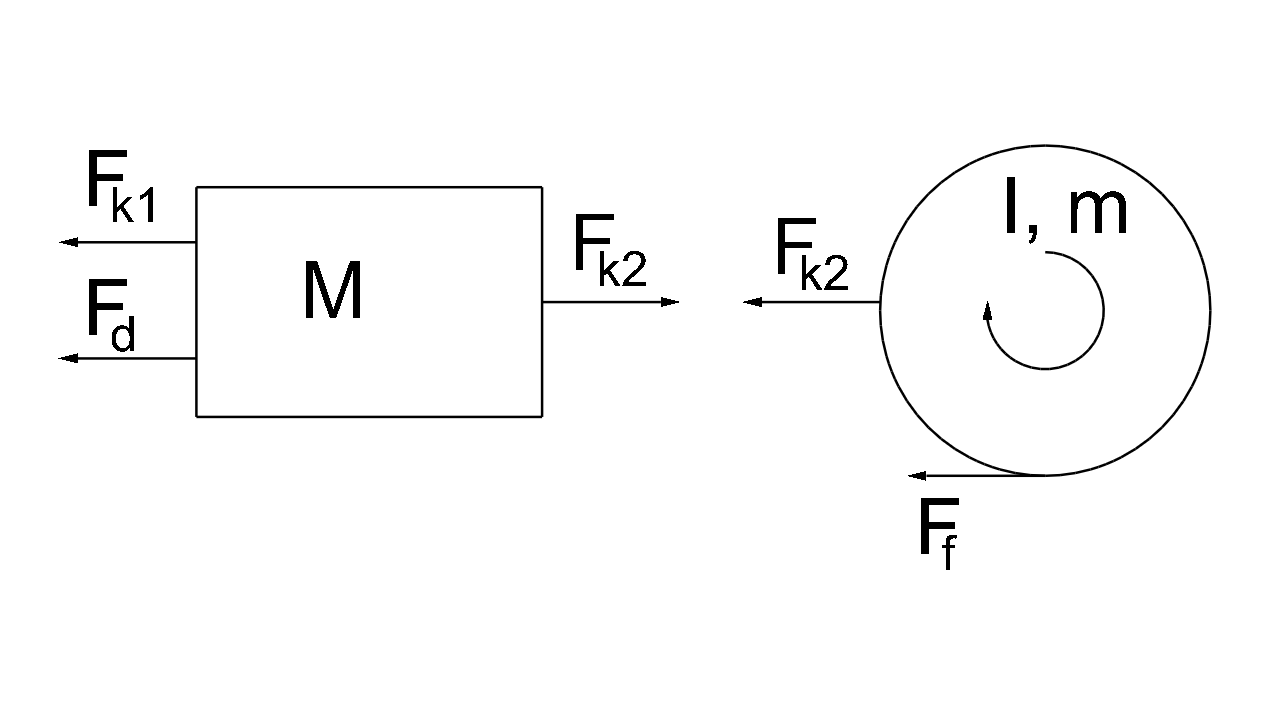
The two bodies in the system are referred to as body 1 (with mass M) and body 2 (with mass m and moment of inertia I). The next step is to draw the free-body diagram for each body, which is shown in Fig. 2↓.