 |
||||||||
 |
 |
 |
 |
|||||
 |
||||||||
 |
||||||||
 |
 |
|||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
ORIENTATION OF A RIGID BODY
Example: Sweep of a wing (Two-dimensional rotation)
Consider a wing that has variable sweep. Let the original, unswept rectangular wing represents the fixed frame with unit vectors (I, J, K), and the axes attached to the wing as it changes sweep are the body-fitted coordinate system, (i, j, k).
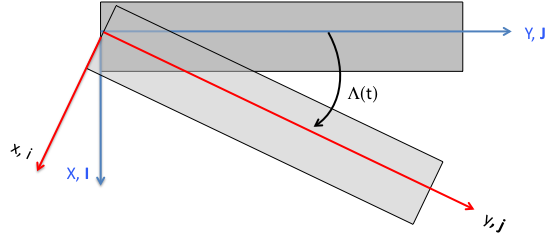
i
=
cos(Λ)I + sin(Λ)J
j
=
− sin(Λ)I + cos(Λ)J
If
X
=
X1 I + X2 J
x
=
x1 i + x2 j
Then the components of the Euler coordinate system can be found in terms of the body-fitted coordinate system by taking the dot product as shown by:
X1
=
(x1 i + x2 j)⋅I
X1
=
x1cos(Λ) − x2sin(Λ)
and
X2
=
(x1 i + x2 j)⋅J
X2
=
x1sin(Λ) + x2cos(Λ)
Example: Aircraft Orientation (Three-dimensional rotation)
The attitude of an aircraft is expressed in the body-fitted coordinate system(i, j, k), while the horizon is set to the Eulerian coordinate system (I, J, K). The Eulerian representation for this transformation can be expressed as
⎧⎪⎨⎪⎩
i
j
k
⎫⎪⎬⎪⎭ = [φ][θ][ψ]⎧⎪⎨⎪⎩
I
J
K
⎫⎪⎬⎪⎭
How can attitude of the aircraft be found in terms of the Eulerian system?
⎧⎪⎨⎪⎩
I
J
K
⎫⎪⎬⎪⎭ = [ ?]⎧⎪⎨⎪⎩
i
j
k
⎫⎪⎬⎪⎭
This is accomplished by inverting the set of rotational matrices: ([φ][θ][ψ]) − 1. Using numerical methods (using a toolbox, for example), this can be shown to be equivalent to the transformation of each matrix, along with a reordering of the matrices.
([φ][θ][ψ]) − 1 = [ψ]T[θ]T[φ]T
This relationship is important, as is discussed in the numerical methods section, the multiplication and inverse of the three rotation matrices is numerically intensive. The transpose of each matrix is easily accomplished by hand by exchanging the matrix elements mij = mji and reordering the matrix order.