ORIENTATION OF A RIGID BODY

Eulerian angles:

X,Y, Z and are a fixed inertial frame.

let x, y, z and i, j, k be fixed to the body such that it will move with the body.

First motion:

 

 

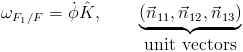
Second motion:

 

 

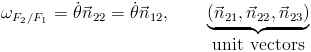
Third motion:

 

 

 

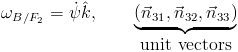
For this to be useful, we need to operate in the same unit vector system.

Let us keep our notation short by denoting sin as S and cos as C.

As now,

This is the rotation w.r.t the moving body. We can do the same procedure and find the rotation w.r.t. the fixed (inertial) frame:

We can break up the rotation as:

We can use these to solve for the rotation of each

,

,