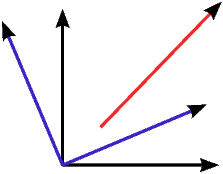
Figure 0.10 two different frame of reference and one unique vector. In this example the black frame rotates to become blue frame. The red vector is physically the same vector and it is independent of frame of reference. One can decide to write the component of this vector in any frame and these components are related to each other through rotation matrix.

For example if a vector e can be written as e = α₁a₁ + α₂a₂ + α₃a₃ = β₁b₁ + β₂b₂ + β₃b₃. α₁, α₂ and α₃ are the components of vector e in frame A. β₁, β₂ and β₃ are the components of vector e in frame B. These componet are related to each other via direction cosine matrix.

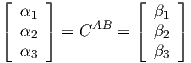(0.6)

Notice that despite the fact that α_i are not equal to β_i, the vector e is one unique vector and shows the same physical phenomena. This concept is used often in dynamics.