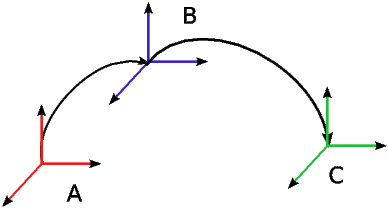
Combination of rotation

Figure 0.6 shows three frames of reference, assuming B rotates in A and C rotates in B. One can calculate rotation matrix that transforms A to C directly with the following formulation.

(0.5)

Non-commutativity of rotation

Finite rotation operations do not commute. This means that the order in which successive finite rotations are applied is important. Figs. 0.7 and 0.8 show an example to illustrate this point. Fig. 0.7 shows two successive rotation, first about green axis and then about blue axis. Fig. 0.8 shows the same rotations in different order so now first rotation is taken place about blue axis and the second one is about green axis. The final result is clearly different from the first case result.

Change of frame of reference

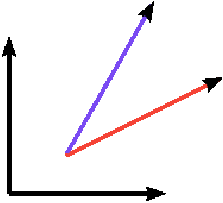
Figure 0.9 shows rotation of a vector. In this case the red vector rotates to become the blue vector. These are two different vectors. This concept is a geometric concept of rotation.