|
||||||||
 |
 |
 |
 |
|||||
 |
||||||||
 |
||||||||
 |
 |
|||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
ROTATION MATRIX
General formulation
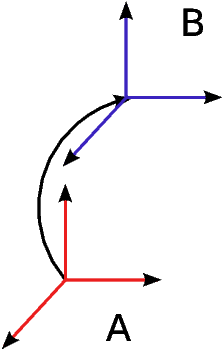
Figure 0.2 shows a more general case, where B frame (the blue one) rotates with respect to A frame about unit vector (n). One can write the direction cosine matrix which brings A frame to B as below
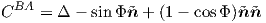 | (0.1) |
where Φ is the rotation angle. This is the result of Euler’s thorem on finite rotations.
Euler’s thorem on finite rotations: Any arbitrary finite rotation that leaves a point
fixed can be viewed as a single rotation of magnitude Φ about a unit vector 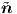 [?].
[?].
Next Page →
Next Page →