Welcome to AE Resources
Converted document Converted document
VELOCITY AND ACCELERATION OF POINTS ON THE SAME BODY
Consider the following example problem.
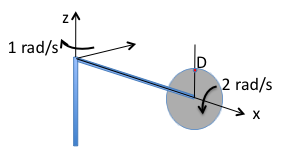
figure images/diskrotating.png
A drop of water, D, is moving towards the center of a disk, B, of radius, r = 0.5ft that is rotating with a constant angular velocity with respect to a fixed frame of reference frame G. The disk is mounted on a bar of 1 ft. that is also rotating at a constant angular velocity. The drop of water is moving at a velocity of 0.02 ft/sec and has an acceleration of 0.01 ft/sec/sec.
The angular velocity of the disk in the fixed frame of reference is a combination of the two rotations:
ωD ⁄ G  =  ωD ⁄ B + ωB ⁄ G       ωD ⁄ G  =  2 i + ( − 1) k
The velocity of the drop of water D with respect to G can be written as V(D)/(G) = V(D)/(B) + V(O’)/(G) + (ω(D)/(G) × rO’D) where O’ is the center of the disk.
The drop of water is moving downward on the disk, so V(D)/(B) =  − 0.02 k. The velocity of the disk with respect to the reference frame is V(O’)/(G) is a rotation about the fixed point on the bar, so the velocity is the angular velocity times the radius or ( − 1)(1) j (the  − 1 is the angular velocity). The distance of the drop is currently the radius of the disk, and the drop is in the positive z direction, so rO’D = 0.5 k. Substituting these values
V(D)/(G)  =  V(D)/(B) + V(O’)/(G) + (ω(D)/(G) × rO’D)       V(D)/(G)  =   − 0.02 k +  − 1 j + (2 i + ( − 1) k) × 0.5 k       V(D)/(G)  =   − 0.02 k +  − 1 j + ( − 1 j + 0)       V(D)/(G)  =   − 2 j − 0.02 k