Welcome to AE Resources

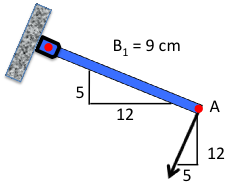
Information about bar one can also be extracted from Fig. 4↑, although it must be applied in a different manner. The direction of the velocity of point A can also be gleaned from the orientation of bar one and the rotation of bar three. This 5-12 triangle also provides some information about the length of the bar in the coordinate directions. The hypotenuse of a 5-12 cm triangle is 13 cm, while the bar length is only 9 cm. The length of the bar in the two coordinate directions can be computed by multiplying the length of the bar (9 cm) by the fractional lengths (i.e., 12/13 i and 5/13 j). Multiplying this out results in lengths of (8.31 i cm and 3.26 j cm)

Figure 6 Evaluation of bar one.

Armed with this information, the system behavior can be computed. Since the angular velocity of bar three is known, the velocity at point B can be computed. The velocity at the pivot (let it be point O) is equal to zero since it has no translation.

V_B + ω₃ × r_BO = 0 V_B( − 4 i − 3 j) + 1.0 k × (3 i − 4 j) = 0 V_B( − 4 i − 3 j) + (3 j + 4 i) = 0 i: V_B( − 4) + (4) = 0 j: V_B( − 3) + (3) = 0 V_B = 1 V_B = − 4 i − 3 j cm/s

In this calculation, the vector for the velocity of point B can be replaced by the magnitude since the direction is already known. Notice that the angular velocity of the body is multiplied by the position vector r_BO. If the vector from r_OB is used instead, the end result will give V_B = − 1, indicating that the velocity is in the opposite direction. A quick look at Fig. 5↑ shows that this is impossible physically. Use of physics to confirm mathematical results (and vice versa) is a very helpful strategy to make a habit. The equation in line 3 has both i and j components. The equation in line 3 can be decomposed into two independent equations since i and j are orthogonal to one another. Solving both equations in lines 4 and 5 yield the same result that V_B = 1. If they do not both give the same result, then there is a mistake in the mathematics. This is another good way to check a calculation for errors. The magnitude can be put together with the earlier direction to yield a final velocity vector for point B of V_B = − 4 i − 3 j cm/s.

Now that the behavior of point B is known, the behavior of bar two and point A can be computed. Since point B is on bars two and three, and point A is on bars one and two, they can related through bar two:

V_A = V_B + ω₂ × r_BA V_A( − 3.26 i − 8.31 j) = ( − 4 i − 3 j) + ω₂ k × 6 j V_A( − 3.26 i − 8.31 j) = ( − 4 − 6ω₂) i − 3 j

Using the knowledge of the velocity of point A from Fig. 6↑, and the known velocity of point B, this equation has components in both i and j and two unknowns. Thus, this should be sufficient to compute the two unknown magnitudes.

The j component only has one unknown, which can be readily solved:

V_A( − 8.3) = − 3 V_A = 0.361 cm/s

Using this result, the i component equation can also be solved:

V_A( − 3.26) = ( − 4 − 6ω₂) 0.361( − 3.26) = ( − 4 − 6ω₂) ω₂ = 0.47 rad/s

Finally, these values can be used on bar one to determine its angular velocity. Let point "P" be the pivot for bar one:

V_A = V_P + ω₁ × r_PA 0.361( − 3.26 i − 8.31 j) = 0 + ω₁ k × (8.31 i − 3.26 j) − 1.18 i − 3 j = ω₁(8.31 j + 3.26 i) i: − 1.18 = ω₁3.26 j: − 3.00 = ω₁8.31 ω₁ = 0.361 rad/s

Once again, the third equation is actually two equations. Solution of either equation (another check) should provide the same answer for ω₁ (within the errors introduced by round off).