|
||||||||
 |
 |
 |
 |
|||||
 |
||||||||
 |
||||||||
 |
 |
|||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
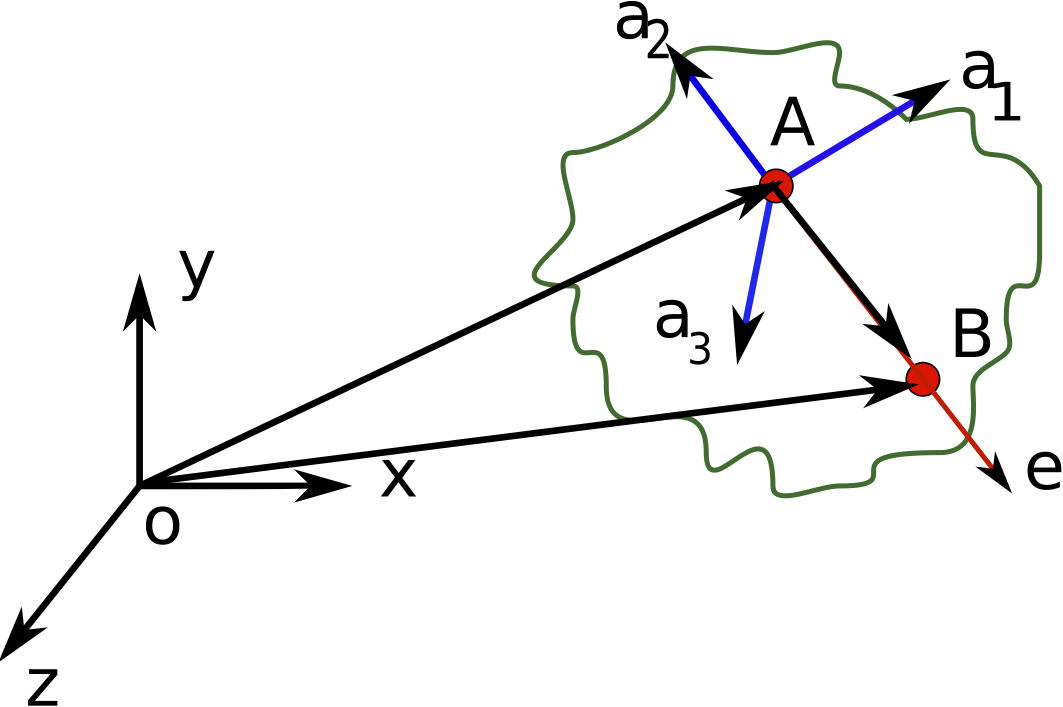
VELOCITY OF TWO POINTS ON THE SAME BODY
If a body is undergoing both translation and rotation, then the vectors that describe the velocity of each point can be different. Figure 2↓ shows an illustration of this scenario. A and B are two arbitrary points on the rigid body. A frame of reference can be attached to this rigid body. Frame a can be defined with a1, a2 and a3 as unit vectors along each axis and point A as the origin. The angular velocity of frame a with respect to inertial or fixed frame (xyz) is denoted by ωa ⁄ I. One can write the following relation between position vectors and point A and B.
(3) POB = POA + PAB
Since velocity is the time derivative of position vector, this equation becomes
where (d)/(dt)POB = VB and (d)/(dt)POA = VA since they are with respect to the frame where the origin O is located (notice O is in the subscript). (d)/(dt)PAB is the relative velocity of B with respect to A, the nomenclature VB ⁄ A to show this term; therefore
(5) VB = VA + VB ⁄ A
Equation (5↑) is true for any arbitrary point A and B, regardless of if they are on the same rigid body or not. If A and B are on the same rigid body then the distance between them is constant. Let e be a unit vector in the direction of PAB, so that the distance can be defined as
(6) PAB = |AB|e
where |AB| is the magnitude of PAB. Since A and B are on the same rigid body so that|AB| is constant, then
Using the chain rule, this becomes
Since |AB| is constant, the underlined term in equation (8↑) is zero. Also the derivative of a unit vector is
(9) (d)/(dt)e = ωa ⁄ I × e
Substituting equation (9↑) into (8↑)
(10) VB ⁄ A = |AB|ωa ⁄ I × e = ωa ⁄ I × |AB|e
and
(11) VB = VA + ωa ⁄ I × e
Since |AB|e is PAB, then
(12) VB = VA + ωa ⁄ I × PAB