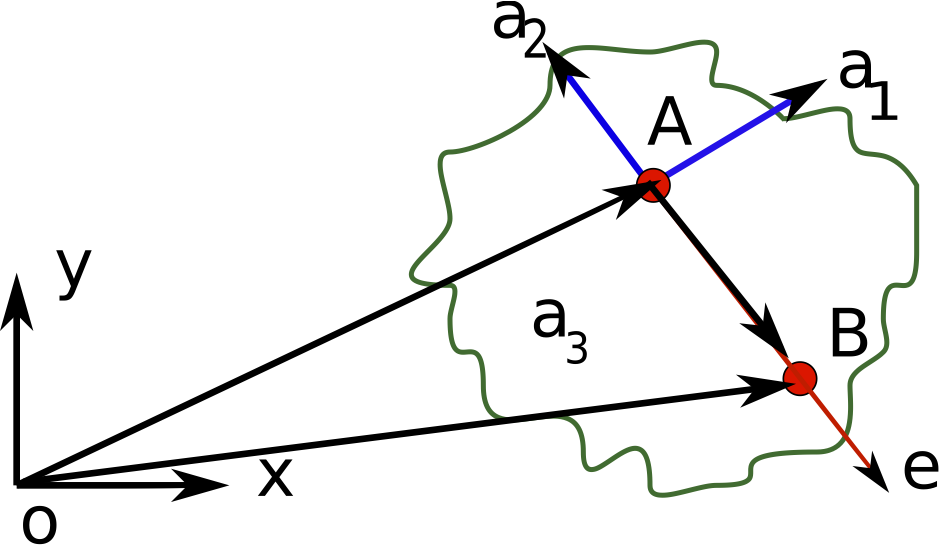
Figure 3↓ shows the same problem but simplified to motion in the x − y plane. ω_a ⁄ I simplifies to θ̇k where k is the unit vector in a₃ or z direction. P_AB is a vector in x − y or a₁ − a₂ plane so that

where the α and β terms represent constants in each coordinate system. Taking the derivatives, and substituting the values from eq.  14↑ the yields