 |
||||||||
 |
 |
 |
 |
|||||
 |
||||||||
 |
||||||||
 |
 |
|||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
EXAMPLE: ROLLING CYLINDER WITH COUPLE
Consider a wheel undergoing the effects of opposite forces, as shown in the figure. The wheel has a mass of 10kg, a radius of 0.4m and a radius of gyration (normal to the plane for the figure), through C of 0.3m. The wheel is initially at rest and does not slip.
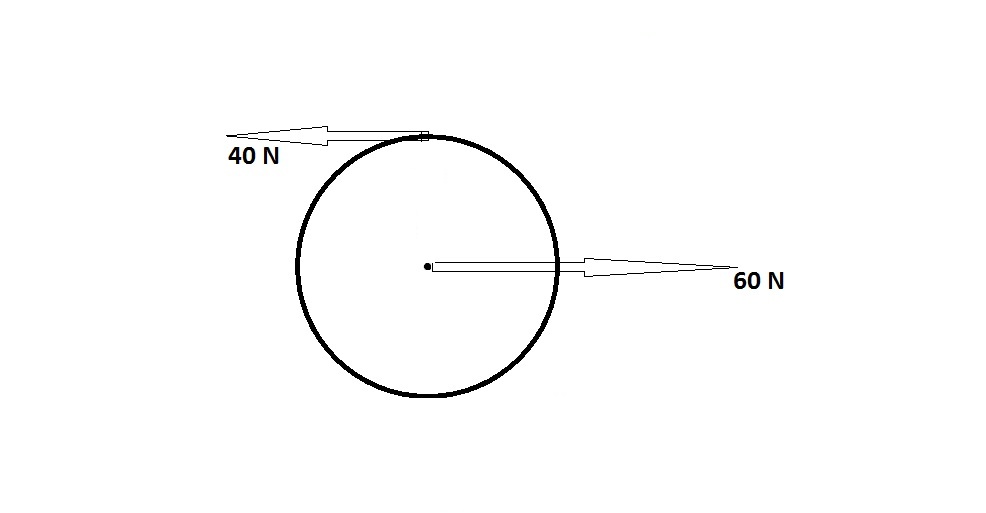
a) Draw and label the free body diagram.
b) Determine the angular acceleration of the wheel.
c) How far does the mass center, C, move in 3 seconds?
d) What is the velocity of C after it has moved 3m.
Solution
a) The free body diagram can be drawn as
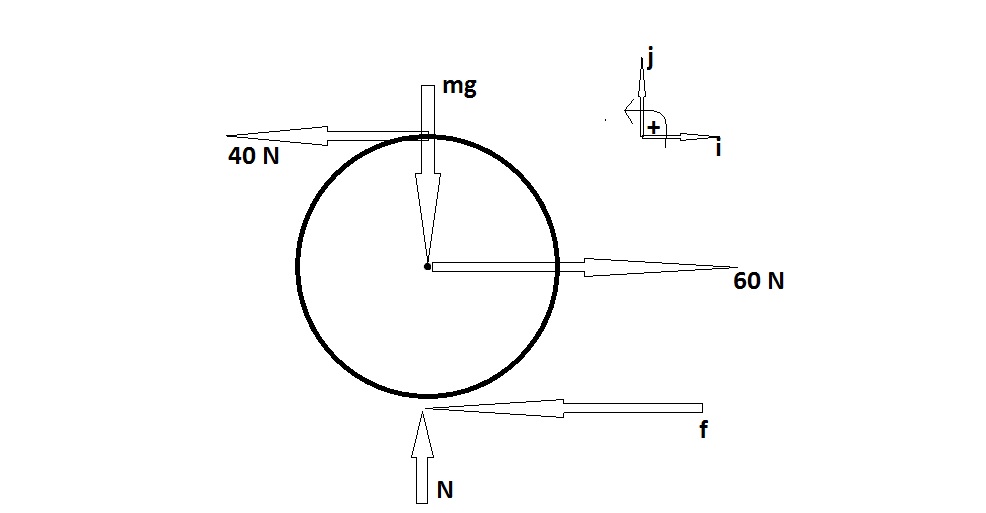

using a Cartesian coordinate system.
⎲⎳Fy
=
0
N
=
mg
⎲⎳Fx
=
mẍc
60 − 40 − f
=
10ẍc
20 − f
=
− 4α
⎲⎳Mc
=
Icα
20(.4) − f(.4)
=
(.3)2α
8 − .4f
=
0.09α
Combining the force in the x direction and the moment equations yields:
8 − 0.4(20 + 4α)
=
0.09α
8 − 8 − 0.16α
=
0.09α
8
=
2.5α
α
=
3.2(r)/(s2)