Welcome to AE Resources
Converted document PRINCIPLE OF WORK AND ENERGY EXAMPLES

PRINCIPLE OF WORK AND ENERGY EXAMPLES

WORK FOR AN INSTANTANEOUS CENTER

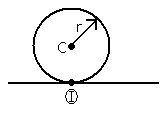
figure images/InstantaneousCenter.png
Figure 1 Circular body of radius r with coordinate axes originating at center point C and an instantaneous center I.
For a rolling circular body, as seen in Figure 1↑, where the velocity of the center VC is moving along one axial direction (VC = VCi), where IC is the moment of inertia about point C, and m is the mass of the body.
The rate of change of kinetic energy is equivalent to power: P = KĖ. The power for this case can be integrated to get the work done on the body:
(1) t2⌠⌡t1Pdt = KE(t2) −  KE(t1) =  KE2 −  KE1
(2) W = ΔKE = ⎡⎣(1)/(2)mV2C + (1)/(2)ICω2⎤⎦t2t1
where external work equals the change in kinetic energy ΔKE.
These calculations assume that the body MUST be rigid (the body does not deform or bend).

WORK FOR A CONTACT POINT

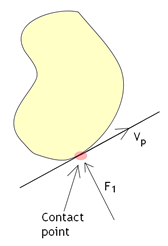
figure images/Contact.png
Figure 2 Arbitrary rigid body on a slope with a point in contact with the ground.
For Figure 2↑, the following steps can be taken to compute the work, W.
  1. For a constant F1 value, W = ∫F1V1dt = F1∫V1dt
  2. F1 is a gravity force and acts on P1. Therefore, F1 = cos(α)mg.
  3. At the contact point, W = ∫F1V1dt = 0. The normal reaction force, F1, always does no work when it is perpendicular to the point of contact.
  4. Vp = 0 at the point of contact. Therefore, W = ∫F1Vpdt = 0.